Question

50 баллов!
Пожалуйста с рисунками


Сколькими способами можно на границе квадратного участка поставить 4 столба
так, чтобы расстояние между ними было не меньше длины стороны участка?​

Answer 1

Ответ:

1 способ

Пошаговое объяснение:

Один способ очевиден - ставим столбы в углах квадрата.

Докажем, что других способов нет. Доказательство от противного.

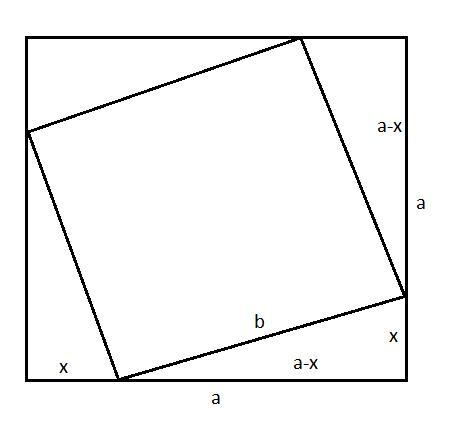
Пусть при некоторой величине x расстояние между столбами будет равно длине стороны квадрата: b = a (смотри рисунок).

Тогда по теореме Пифагора

x^2 + (a - x)^2 = a^2

x^2 + a^2 - 2ax + x^2 = a^2

2x^2 - 2ax = 0

x^2 - ax = 0

x1 = 0; x2 = a

Как видим, получился отрезок х = а, то есть стороне квадрата.

Это и означает, что столбы должны стоять в углах квадрата.