Предмет: Алгебра,
автор: Змия14
Вычислить площадь фигуры, ограниченной линиями.
ПОЖАЛУЙСТА ПОМООООГИТЕ ОЧЕНЬ НАДО ДАМ 25 БАЛЛОВ
Приложения:
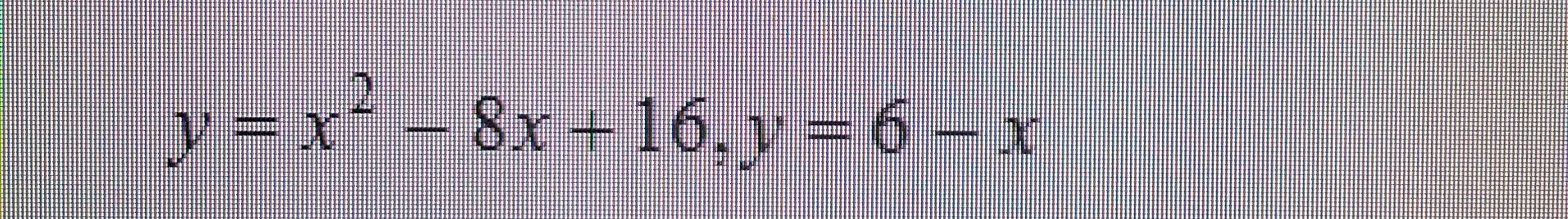
Ответы
Автор ответа:
1
Дано: F(x) = x² - 8*x + 16, y(x)= -x+6
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков: F(x)=y(x).
- x²+7*x -10=0 - квадратное уравнение
b = 5 - верхний предел, a = 2 - нижний предел.
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) = 10 -7*x + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
∫s(x) = 10*x -7/2*x² + 1/3*x³
4) Вычисляем на границах интегрирования.
S(b) = S(5) = 50 - 87 1/2 + 41 2/3 = 4 1/6
S(a) = S(2) = 20 - 14 + 2 2/3 = 8 2/3
S = S(2) - S(5) = 4,5(ед.²) - площадь - ответ
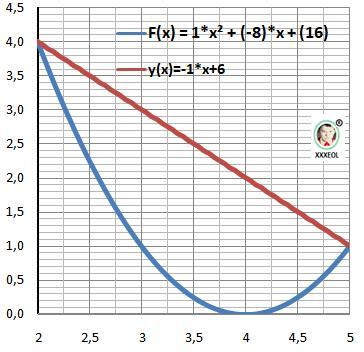
Рисунок к задаче в приложении.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: pamkus
Предмет: Литература,
автор: dimk4ch
Предмет: Алгебра,
автор: mamadimamoi891024
Предмет: Алгебра,
автор: Stryker2000
Предмет: Математика,
автор: Аноним