Question

Срочно!Помогите пожалуйста)

Answer 1

Решение задания приложено

Answer 2

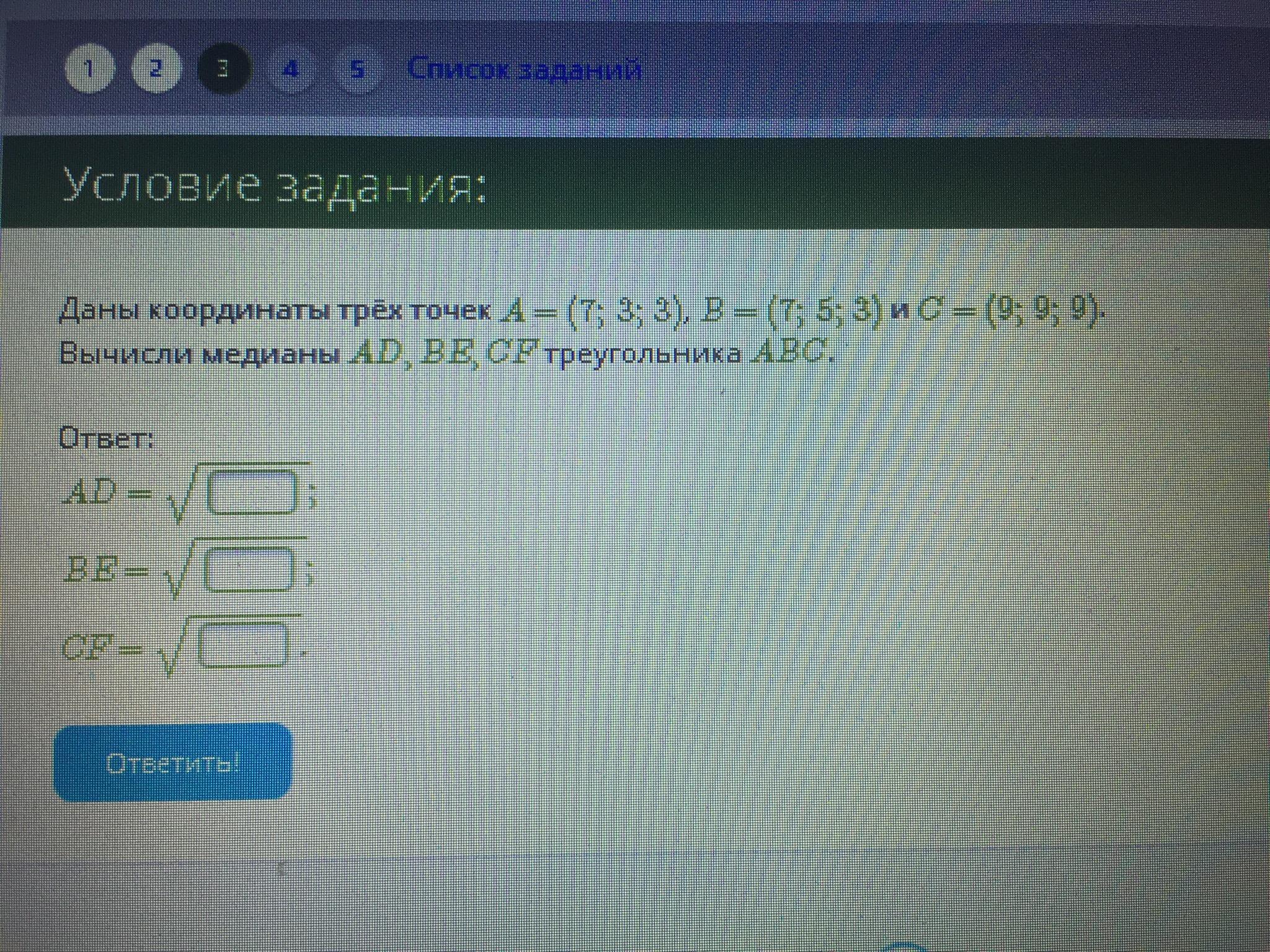
Дан треугольник, который находиться в трёхмерном пространстве и вершины которого A(7;3;3), B(7;5;3), C(9;9;9).

Так как по определению, медиана – это прямая, которая делит отрезок на 2 равных, то точка, которая пересекает отрезок будет его центром, а значит её координаты мы найдём по формуле:

$x = \frac{a_{x} + b_{x}}{2} \\ y= \frac{a_{y} + b_{y}}{2} \\ z = \frac{a_{z} + b_{z}}{2}$

Необходимо найти медианы AD, BE, CF, значит DєBC, EєAB, FєAC, причем D – средина BC, E – средина AB, F – средина AC.

Находим координаты этих точек по вышеприведённой формуле:

D(8;7;6), E(8;6;6), F(7;4;3)

Теперь мы можем найти саму медиану как расстояние между начальной и конечной её точками.

Медиана AD:

$ad = \sqrt{(x_{d} - x_{a})^{2} + (y_{d} - y_{a})^{2} + (z_{d} - z_{a})^{2}} \\ ad = \sqrt{(8 - 7)^{2} + (7 - 3)^{2} + (6 - 3)^{2}} \\ ad = \sqrt{1 + 16 + 9} \\ ad = \sqrt{26}$

Медиана BE:

$be = \sqrt{(x_{e} - x_{b})^{2} + (y_{e} - y_{b})^{2} + (z_{e} - z_{b})^{2}} \\ be = \sqrt{(8 - 7)^{2} + (6 - 5)^{2} + (6- 3)^{2}} \\ be = \sqrt{1 + 1 + 9} \\ be = \sqrt{11}$

Медиана CF:

$cf= \sqrt{(x_{f} - x_{c})^{2} + (y_{f} - y_{c})^{2} + (z_{f} - z_{c})^{2}} \\ cf = \sqrt{(7 - 9)^{2} + (4 - 9)^{2} + (3 - 9)^{2}} \\ cf= \sqrt{4 + 25 + 36} \\ cf = \sqrt{65}$

Ответ: AD = √26, BE = √11, CF = √65.