Предмет: Математика,
автор: zhdanovakseniyapak1
Помогите пожалуйста решить!!!
Приложения:
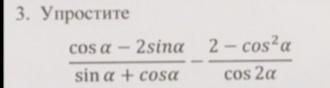
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: cobotokirina336
Предмет: Английский язык,
автор: akjshsiskdndjksjddh
Предмет: Литература,
автор: solomiamusnina
Предмет: Математика,
автор: Eva1111111111111111
Предмет: Математика,
автор: Аноним
В числителе выделяем синус двойного угла и всё сокращается в тангенс двойного угла.