Предмет: Алгебра,
автор: Аноним
Допоможіть будь ласка
Приложения:
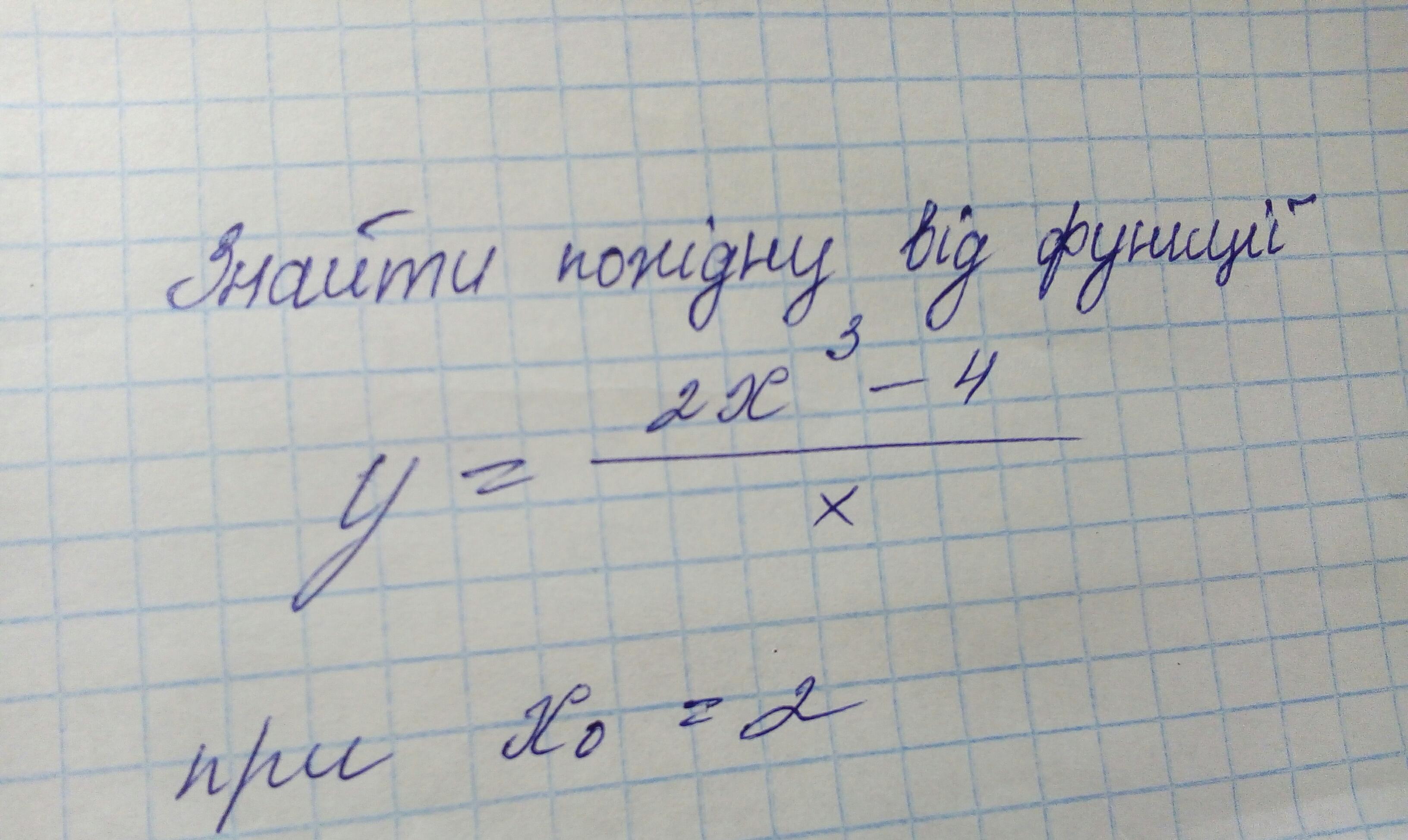
Ответы
Автор ответа:
0
Дана функція
Запишем функцію в іншому вигляді, для легшого диференціювання:
Знаходемо похідну ( y' = g(x) ):
Тепер знаходимо значення похідної в точці х0 = 2:
Відповідь: 9.
Аноним:
Потрібно по іншій формулі...
(u/v)'= (u-v)-(u-v)'/v
Похожие вопросы
Предмет: Биология,
автор: standofftop277
Предмет: Литература,
автор: ishanovav2004
Предмет: Алгебра,
автор: yuliyakoryakina89
Предмет: Математика,
автор: veronika88881
Предмет: Геометрия,
автор: Рахат11122233