Предмет: Алгебра,
автор: кармини
Найти производную!!!!
Приложения:
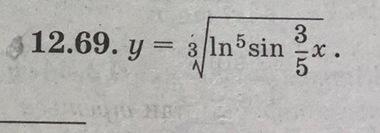
Ответы
Автор ответа:
1
Ответ:
=============================
Объяснение:
Приложения:
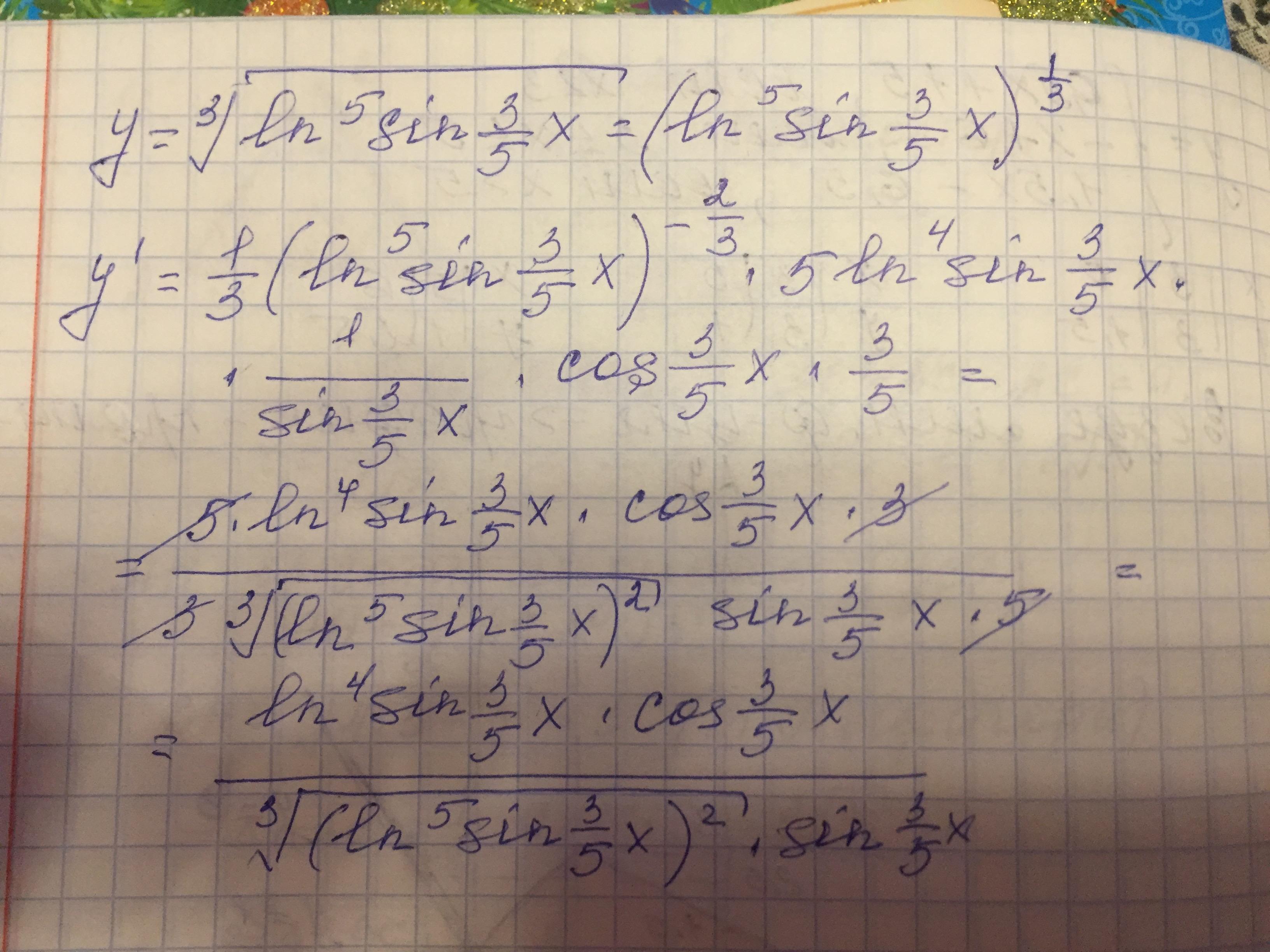
кармини:
Большое спасибо!) Очень хорошее объяснение)
формально ответ написан верно. хотя я бы взял в скобки логарифм в четвертой от синуса трех пятых икс. т.к. получается, вы умножаете синус на косинус, а на самом деле умножение четвертой степени логарифма на косинус........... эдакого аргумента.
Автор ответа:
0
Представим функцию, как степенную с показателем 1/3,
y=(㏑⁵(sin(0.6x)))¹/³
(u¹/³)'=(1/3)u'*u⁻²/³, в качестве u выступает пятая степень логарифма от
sin( 0.6х), поэтому находим производную еще от одной степенной, (u⁵)'=5u'*u⁴, потом от логарифмической функции (㏑u)'=u'/u, теперь в качестве u выступает sin( 0.6х), производная которого равна косинусу от того же аргумента, умноженная на производную от (0.6х), которая равна 0.6.
Итак. искомая производная равна
(1/3)*(㏑⁵(sin(0.6x)))⁻²/³*(5㏑⁴(sin(0.6x)))*(1/(sin(0.6x))*(cos(0.6x))*(0.6)
Похожие вопросы
Предмет: Математика,
автор: pankratovavioletta9
Предмет: Биология,
автор: Mockevicius82
Предмет: Математика,
автор: aminaartygolieva
Предмет: Химия,
автор: danilyakutsksit
Предмет: История,
автор: 67493823