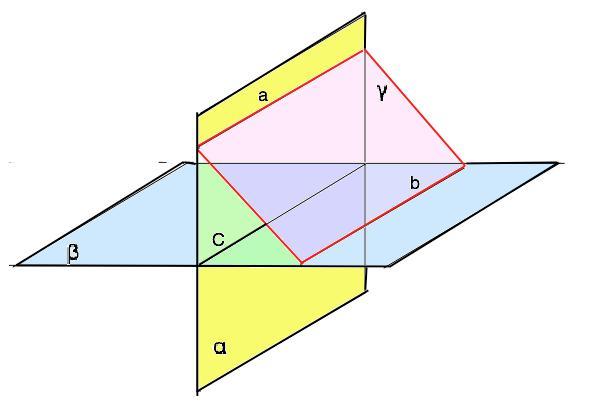
Плоскости альфа и Бетта пересекаются по прямой C. Поскостъ гамма, параллельная прямой С, пересекает плоскости альфа и Бетта по прямым а||b соответственно. Докажите, что а|| Бетта b || альфа
Рисунок тоже, пожалуйста
Ответы
Если плоскость проходит через данную прямую , параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Плоскость α проходит через прямую С, параллельную плоскости γ, и пересекает эту плоскость, => линия пересечения а плоскостей α и γ параллельна прямой С. => а||С
Из теоремы о параллельности прямой и плоскости:
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Прямая а не лежит в плоскости β и параллельна прямой С, лежащей в плоскости β, значит, прямая а параллельна плоскости β.
Аналогично плоскость β проходит через прямую С, параллельную плоскости γ, пересекает плоскость γ, => линия пересечения b плоскостей β и γ параллельна прямой С. => b || С, значит, b || α.
Доказано.