Question

В прямоугольной трапеции ABCD
AD|| BC, AB = 4, AD = 7, уголD = 45°.
Найдите длины векторов ВС, CD и BD.​

Answer 1

Ответ: BC=3

CD=$\sqrt{32}$

BD=$\sqrt{65}$

Объяснение:

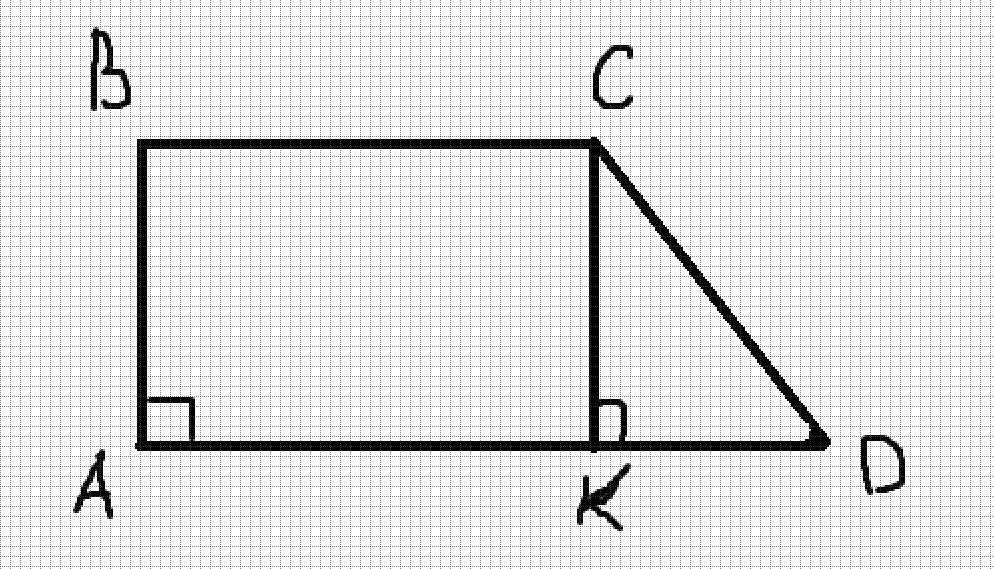
Смотри рисунок. угол  BDC = 45 градусов из условия задачи. Я достраиваю высоту CK так как это высота то угол CKD=90 градусов а из этого следует что угол KCD = 180-90-45=45 а это значит что треугольник CKD равнобедренный то есть CK=KD. ABCK прямоугольник по этому AB=CK=4 см а так как CK=KD то KD=4 см тоже а теперь по теореме Пифагора можно найти гипотенузу прямоугольного треугольника CD=$\sqrt{4^{2}+4^{2}}=\sqrt{32}$

AK=BC=AD-KD=7-4=3

Осталось найти BD найдем так же через теорему Пифагора так как треугольник BAD прямоугольный и нам известны 2 его стороны то есть AD=7 и AB=4 значит BD=$\sqrt{16+49}=\sqrt{65}$