Question

Ребята, прошу помогите! Очень надо!

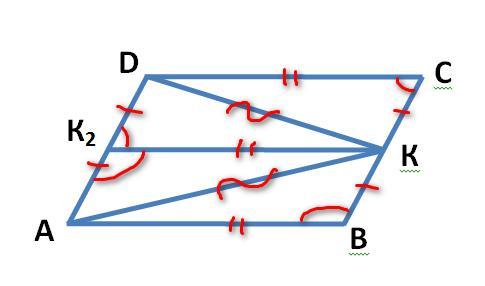
Дан параллелограмм ABCD, точка K принадлежит стороне BC, отрезок BK=KC. Площадь параллелограмма 24(см2). Найти площадь треугольника AKD

Answer 1

Ответ: 12

Объяснение:

Так как ABCD параллелограмм то его противоположные стороны равны. Тоесть DC=AB и CB=AD далее построим точку К2 лежащую на стороне AD и делящей эту сторону пополам так как AD=CB то BK=KC=AK2=K2D. K2K делит ABCD пополам и K2K=DC=AB. Треугольники ABK=DCK=AK2K=DK2K по тому что у них равны 2 стороны и угол между этими двумя сторонами. Так как эти треугольники равны то и их площади равны. площадь параллелограмма складываетсья из 4 площадей данных треугольников по этому полщадь одно треугольника равна 24/4=6 а так как треугольник AKD состоит из 2 таках треугольников то его площадь равна 6*2=12