Предмет: Алгебра,
автор: 4blbru
Помогите с алгеброй
Приложения:
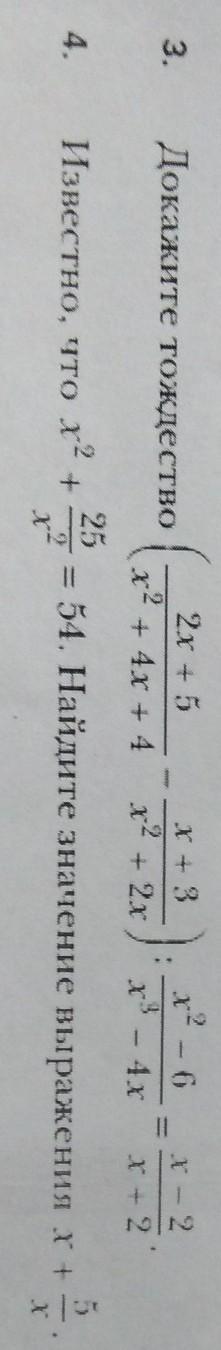
Ответы
Автор ответа:
2
Ответ:
Объяснение:
тождество доказано
Похожие вопросы
Предмет: Химия,
автор: melonaaa
Предмет: Математика,
автор: rrrsaus9
Предмет: Українська мова,
автор: milka30186
Предмет: Математика,
автор: DJ20177
Предмет: География,
автор: Ававааваав