Предмет: Математика,
автор: asvatolina98
Найти общее решение уравнения
Приложения:
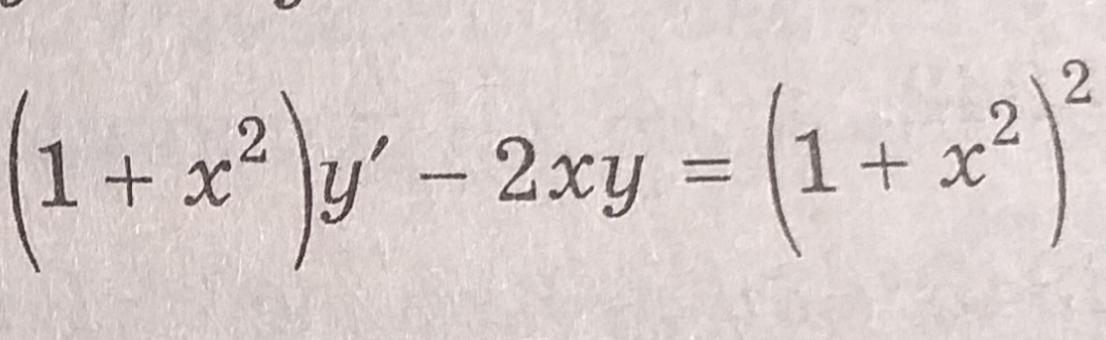
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Информатика,
автор: frooz1k
Предмет: Литература,
автор: iskiss678
Предмет: Математика,
автор: 34tankf
Предмет: География,
автор: anytakot1404
Предмет: История,
автор: Лэна11