Предмет: Алгебра,
автор: qewewrt
решите систему уравнений методом подстановки
Приложения:
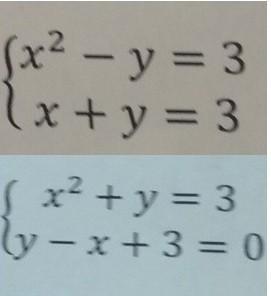
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1)
2)
Похожие вопросы
Предмет: Математика,
автор: stesha34
Предмет: Литература,
автор: alinagus060908
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: senyaresh
Предмет: Литература,
автор: 63464585