Предмет: Алгебра,
автор: vosstanovlenie265017
Решите неравенство и вычислите сумму всех целых решений
Приложения:
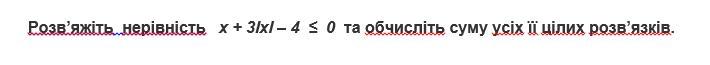
Ответы
Автор ответа:
0
Первый случай:
Второй случай:
Объединение промежутков: хє[-2;1]
Тогда сумма всех целых решений:
Ответ: -2
Universalka:
- 2 + ( - 1) + 0 + 1 = - 2 Почему два раза + 1 ?
Да-да, это я по ошибке 2 раза 1 написал, сорян, виноват
Автор ответа:
0
x + 3|x| - 4 ≤ 0
1) x < 0
x - 3x - 4 ≤ 0
- 2x ≤ 4
x ≥ - 2
x ∈ [- 2 ; 0)
2) x ≥ 0
x + 3x - 4 ≤ 0
4x ≤ 4
x ≤ 1
x ∈ [0 ; 1]
Результат двух решений : x ∈ [- 2 ; 1]
- 2 + (- 1) + 0 + 1 = - 2
Ответ : - 2
Похожие вопросы
Предмет: Музыка,
автор: Nikita277334
Предмет: Музыка,
автор: demanovazena006
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: Ясминуль