Question

Найдите множество значений функции:

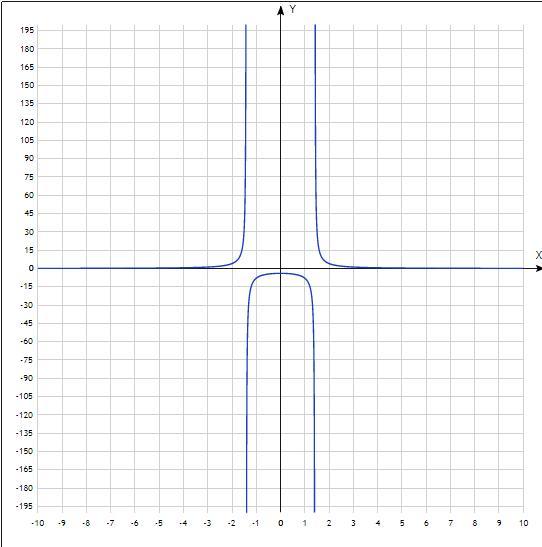
y=8/(x²-2)

Answer 1

Найдите множество значений функции:

y=8/(x²-2)

исследуем данную функцию:

1) область определения

х≠±√2

2) Нули функции : нет.

Значит функция не пересекает ось Ох

Пересечение с осью Оу в точке (0;-4)

3) найдем производную

$\displaystyle y`=(8*(x^2-2)^{-1})`=8*(-1)(x^2-2)^{-2}*2x=\frac{-16x}{(x^2-2)^2}$

Найдем точки экстремума

y`=0 при х=0

__+____ -√2___+_____0___-____+√2__-____

возр.                   возр            убыв             убыв

тогда точка х=0 точка максимума у(0)= -4

4) теперь проверить пределы

$\displaystyle  \lim_{x \to \infty} f(x)=+0\\\\ \lim_{x \to \ -oo} f(x)=+0\\\\ \lim_{x \to \ \sqrt{2}_{+0}} f(x)=+oo\\\\ \lim_{x \to \ \sqrt{2}_{-0} } f(x)=-oo\\\\ \lim_{x \to \ -\sqrt{2}_{+0} } f(x)=+oo\\\\ \lim_{x \to \ -\sqrt{2}_{-0}} f(x)= -oo$

Тогда множество значений (-∞;-4]∪(0;+∞)