Предмет: Алгебра,
автор: malikaasanova92
решите пожалуйста
ответ 1
Приложения:
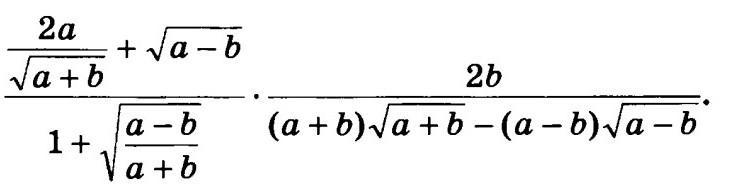
Ответы
Автор ответа:
4
Ответ:
Объяснение:
Похожие вопросы
Предмет: Математика,
автор: ttayya
Предмет: Русский язык,
автор: ld50kukushka
Предмет: Математика,
автор: LimonchikPro
Предмет: Алгебра,
автор: Chubavladislav