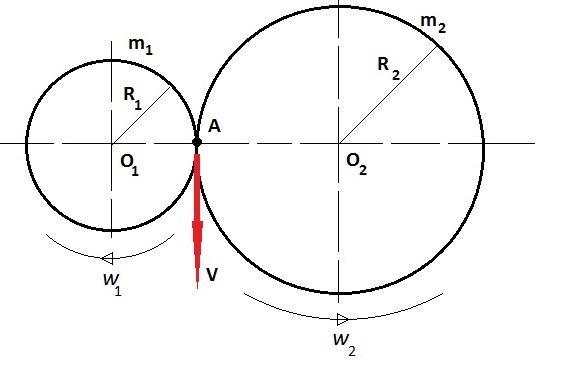
Буровая установка приводится в движение двумя большими, зацепленными друг за друга зубчатыми колёсами на неподвижных осях, имеющими форму тонких обручей радиусов R1 и R2. Массы колёс - m1 и m2 соответственно, причём массой, сосредоточенной в спицах и осях колёс можно пренебречь. Чтобы раскрутить колёса (без приведения в движение других частей установки) пришлось совершить работу A. Найдите угловую скорость ω вращения первого колеса.
Дайте ответ для R1 = 2.5 м, R2 = 5.0 м, m1 = 320.0 кг, m2 = 900.0 кг, A = 30.0 кДж в 1/с с точностью до десятых
Ответы
Ответ:
2,8 рад/с
Объяснение:
Дано:
R₁ = 2,5 м
R₂ = 5,0 м
m₁ = 320 кг
m₂ = 900 кг
A = 30 кДж = 30 000 Дж
___________
ω₁ - ?
1)
Поскольку колеса находятся в зацеплении, то линейная скорость точки А равна
V = V₁ = V₂
V₁ = ω₁·R₁ (1)
V₂ = ω₂·R₂ (2)
Приравняем (2) и (1)
ω₂·R₂ = ω₁·R₁
ω₂ = (R₁/R₂)·ω₁ = (2,5/5,0)·ω₁ = 0,5·ω₁
2)
Считаем зубчатые колеса тонкими обручами найдем их моменты инерции:
J₁ = m₁·R₁² = 320·2,5² = 2 000 кг·м²
J₂ = m₂·R₂² = 900·5² = 22 500 кг·м²
3)
Кинетические энергии колес:
T₁ = J₁·ω₁²/2 = 2000·ω₁² / 2 = 1000·ω₁²
T₂ = J₂·ω₂²/2 = 22 500·0,5²ω₁²/2 ≈ 2810·ω₁²
Суммарная кинетическая энергия:
T = T₁+T₂ = 1000·ω₁² + 2810·ω₁² = 3 810·ω₁² Дж
4)
По закону сохранения энергии:
T = A
3 810·ω₁² = 30 000
ω₁ = √ (30 000 / 3810) ≈ 2,8 рад/с