Прямая задана общим уравнением. Написать ее каноническое и параметрическое уравнение:
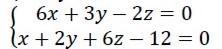
Ответы
Ответ: (x+4)/22=(y-8)/(-38)=z/9
Пошаговое объяснение:
В данном случае прямая задана пересечением плоскостей.
1) для составления канонического уравнения нужно найти точку, через которую проходит данная прямая, и направляющий вектор этой прямой.
Положим z=0, тогда система уравнений, задающая прямую, примет вид:
6*x+3*y=0
x+2*y=12
Решая её, находим x=-4 и y=8. Таким образом, найдена точка М(-4; 8; 0), которая принадлежит прямой. Для нахождения направляющего вектора прямой P заметим, что он ортогонален нормальным векторам N1 и N2 пересекающихся плоскостей и равен их векторному произведению: P=N1xN2. А его можно записать в виде определителя:
N1xN2= i j k , где N1x=6, N1y=3, N1z=-2, N2x=1, N2y=2, N2z=6 -
N1x N1y N1z координаты направляющих векторов, а i, j, k -
N2x N2y N2z орты (единичные векторы) координатных осей.
Подставляя координаты векторов, получаем определитель i j k
6 3 -2
1 2 6,
раскладывая который по первой строке, находим P=22*i-38*j+9*k=Px*i+Py*j+Pz*k . Теперь составим каноническое уравнение прямой по точке M (Mx; My; Mz) и направляющему вектору P:
(x-Mx)/Px=(y-My)/Py=(z-Mz)/Pz. Подставляя известные значения, приходим к уравнению (x+4)/22=(y-8)/(-38)=z/9.