Предмет: Математика,
автор: DEADЕYE
Решите неопределенный интеграл
Приложения:
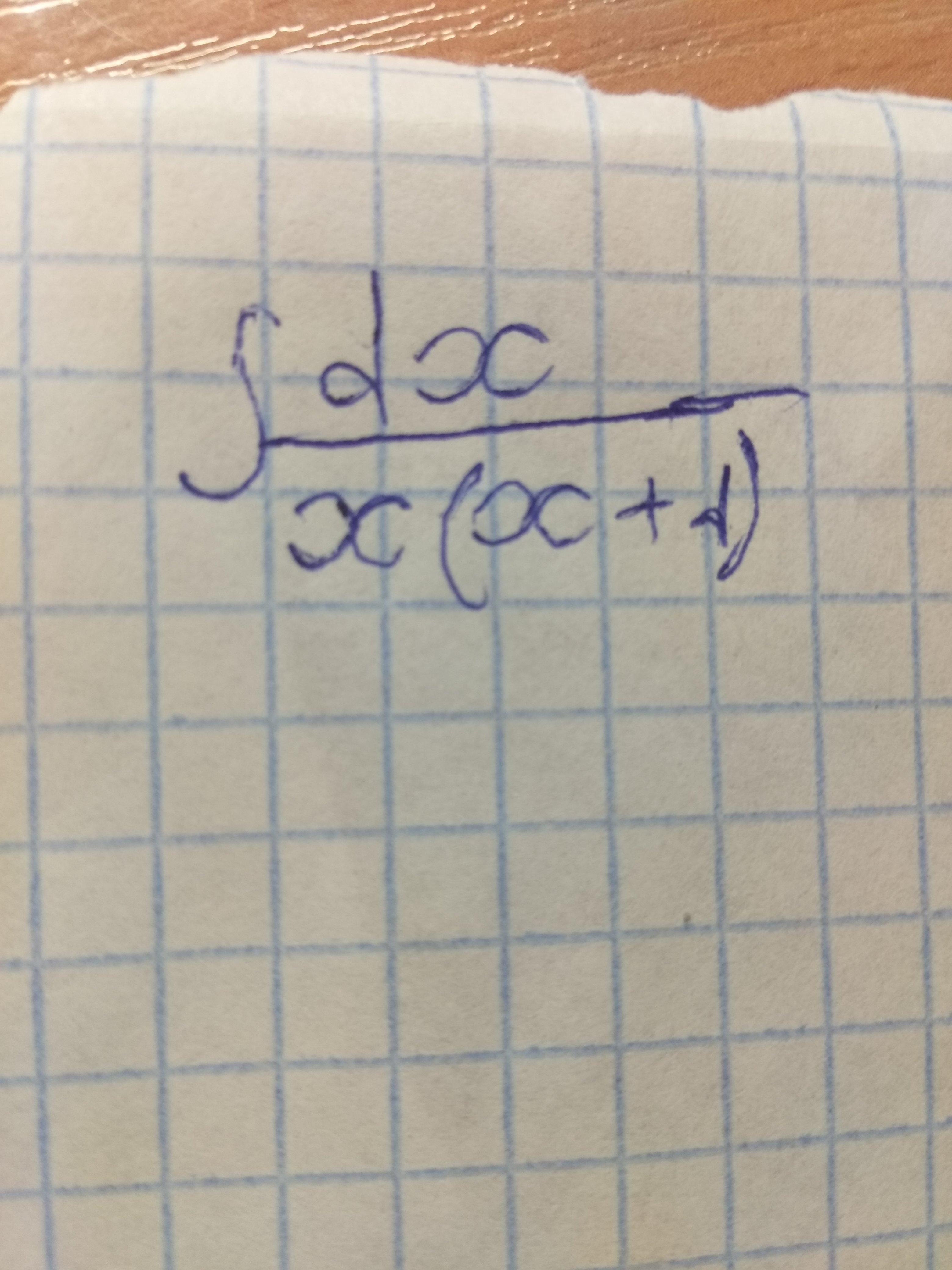
Ответы
Автор ответа:
1
Преобразуем подинтегральную функцию (сначала в числителе прибавим и вычтем х, потом сделаем почленное деление и проведем сокращение):
Таким образом
DEADЕYE:
Почему вместо dx стало 1 ?
Потому что подинтегральная функция не dx/(x(x+1)), а 1/(х(х+1)). dx - это символ того, что интегрирование идет по переменной х.
Понятно, Спасибо большое
пожалуйста!
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: flateee57
Предмет: Английский язык,
автор: swytlanka
Предмет: Алгебра,
автор: смитвапркенг
Предмет: Математика,
автор: SlimShady1111