Предмет: Алгебра,
автор: demidov1006
Решите и если возможно с проверкой
Приложения:
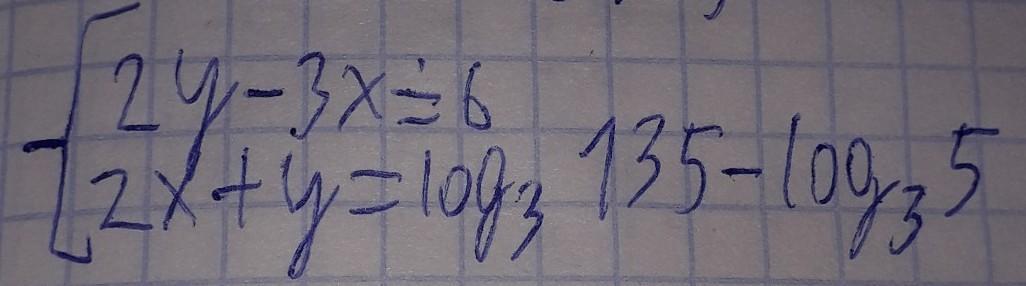
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: andriygal99
Предмет: Русский язык,
автор: varvara1s
Предмет: Английский язык,
автор: Softwareeeee
Предмет: Математика,
автор: Elsa04
Предмет: География,
автор: Lizzztv199