Предмет: Алгебра,
автор: aidarsun
Нужно вычислить интеграл, лучше, если с полным решением
Приложения:
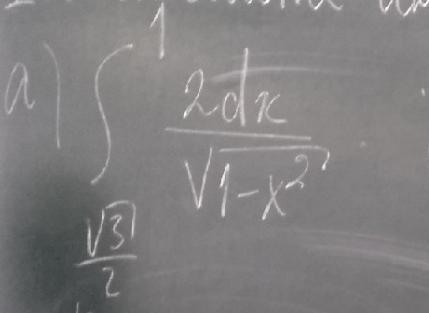
Ответы
Автор ответа:
1
Ответ:
Объяснение:
По формуле:
Похожие вопросы
Предмет: Українська мова,
автор: bat69evelongmailcom
Предмет: Математика,
автор: falieva335
Предмет: Математика,
автор: maskaevaeva278
Предмет: Математика,
автор: Сухарик15