Предмет: Математика,
автор: arkadiysudakov00
Помогите решить пожалуйста.лучше с подробным расписание решения
Приложения:
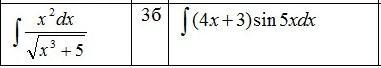
Ответы
Автор ответа:
1
Ответ:
1)
2)
Пошаговое объяснение:
1)
2)
Для нахождения интеграла нужно использовать формулу интегрирования по частям:
где ,
Нужно найти дифференциал , используя
, вычислить
при помощи
и подставить
и
arkadiysudakov00:
Во втором задании если честно,не до конца понял после чего надо писать ответ ? после +C в конце ?
Последнее выражение после последнего знака равенства является ответом (в котором мы произвели интегрирование и соответственно в результате этого появилась константа С).
Дальнейшие алгебраические преобразования на ваше усмотрение.
А это 100% правильно решение ?)
Да
Помогите решить другие мои примеры по данной тематике.буду благодарен.
Похожие вопросы
Предмет: Алгебра,
автор: turnatana1975
Предмет: Математика,
автор: stefani323
Предмет: Русский язык,
автор: sakurailove323
Предмет: Литература,
автор: marina19823
Предмет: История,
автор: sashaparamonov4