Предмет: Алгебра,
автор: badgurll
надо решить это задание,помогите пожалуйста
Приложения:
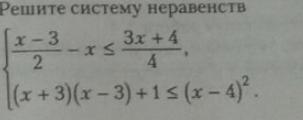
Ответы
Автор ответа:
2
Ответ:держи
Объяснение:
Приложения:

Автор ответа:
1
Ответ: х ∈ [-2; 3]
Похожие вопросы
Предмет: Физика,
автор: lika19900
Предмет: Информатика,
автор: eeeeeetuy
Предмет: Обществознание,
автор: Renat08Ramazanov09
Предмет: Математика,
автор: COBETNIK
Предмет: История,
автор: alabushevden