Предмет: Математика,
автор: marshall963
найти наибольшую сумму x + y, где x и y -цифры числа 71x1y, которое делятся на 45.
Приложения:
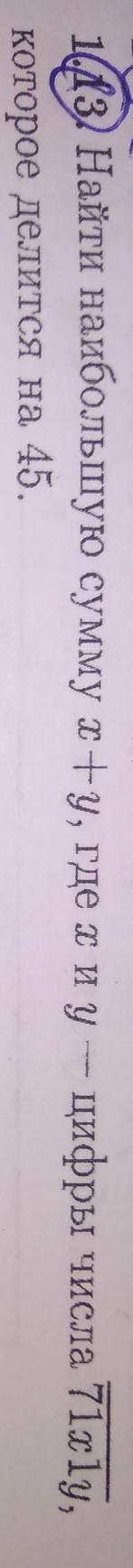
Ответы
Автор ответа:
1
Ответ:
9
Пошаговое объяснение:
Так как 45=5·9, то применим признаки делимости на 5 и 9.
Признак делимости на 5: Число делится на 5 ⇔ последняя цифра делится на 5.
Признак делимости на 9: Число делится на 9 ⇔ сумма его цифр делится на 9.
Чтобы число 71x1y делился на 5 цифра y=0 или y=5.
Сумму цифр числа 71x1y: 7+1+х+1+у=9+х+у. 9 делится на 9, поэтому х+у должен делится на 9. Если у=0 то х=9, если у=5, то х=4, в обоих случаях х+у=9.
Похожие вопросы
Предмет: Физика,
автор: ajnebatocyrenova
Предмет: Астрономия,
автор: ilyalomaev146
Предмет: Математика,
автор: uliageenko7
Предмет: Математика,
автор: eroperop3535
Предмет: Математика,
автор: крис674