Предмет: Математика,
автор: paylinatwy34
Помогите решить срочно!!!!
Приложения:
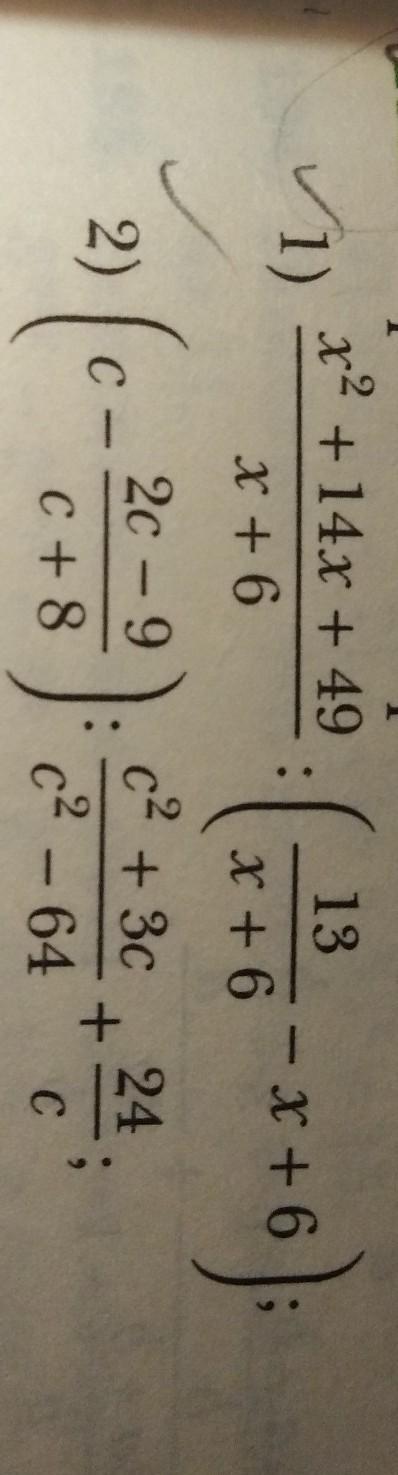
Ответы
Автор ответа:
1
Пошаговое объяснение:
papagenius:
первый исправил
Похожие вопросы
Предмет: Қазақ тiлi,
автор: kamal2575
Предмет: Английский язык,
автор: Аноним
Предмет: Физика,
автор: Cpook
Предмет: Математика,
автор: laradenisenko
Предмет: Математика,
автор: математика597