Question

40 баллов, условия на фото

Answer 1

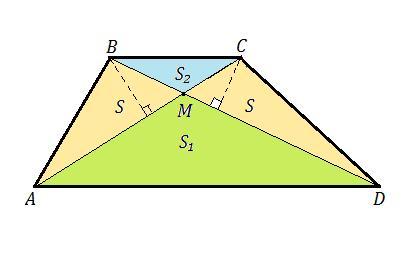
АВСD - трапеция, АD и ВС - основания, АD || ВС , АС и ВД - диагонали , M=АС ∩ ВД ,  S(АDМ)=S₁  , S(BCM)=S₂ .

Док-ть, что   $S(ABCD)=(\sqrt{S_1}+\sqrt{S_2})^2$  .

1.  Рассм. ΔАВD и ΔACD. Их площади равны, т.к. у них одинаковое основание AD и равные высоты ( высоты этих треугольников равны высоте трапеции).  S(ABD)=S(ACD). Отсюда следует, что

S(ABM)=S(CDM) , т.к. S(ABM)=S(ABD)-S(AMD)=S(ACD)-S(AMD)=S(CDM) .

Обозначим  S=S(ABM)=S(CDM) .

2.  Рассм. ΔАВМ и ΔВСМ . У этих треугольников равны высоты, проведённые из вершины В . Поэтому их площади относятся как их основания:

    $\frac{S(BCM)}{S(ABM)}=\frac{0,5\cdot h_1\cdot CM}{0,5\cdot h_1\cdot AM}=\frac{CM}{AM}\; \; \Rightarrow \; \; \; \frac{S_2}{S}=\frac{CM}{AM}$

3.  Aналогично, для треугольников ВСМ и DCM:

     $\frac{S(BCM)}{S(DCM)}=\frac{0,5\cdot h_2\cdot BM}{0,5\cdot h_2\cdot DM}=\frac{BM}{DM}\; \; \Rightarrow \; \; \; \frac{S_2}{S}=\frac{BM}{DM}$

4.  Рассм. ΔВСМ и ΔADM.  ∠ВМС=∠AMD ( как вертикальные). Запишем отношение площадей этих треугольников по формуле, использующей синус угла:

$\frac{S(BCM)}{S(ADM)}=\frac{0,5\cdot BM\cdot CM\cdot sin\angle BMC}{0,5\cdot AM\cdot DM\cdot sin\angle AMD}=\frac{BM\, \cdot \, CM}{AM\, \cdot \, DM}=\frac{CM}{AM}\cdot \frac{BM}{DM}\; \; \Rightarrow \\\\\frac{S_2}{S_1}=\frac{S_2}{S}\cdot \frac{S_2}{S}\; \; \Rightarrow \; \; \; \frac{S_2}{S_1}=\frac{S_2^2}{S^2}\; \; \Rightarrow \; \; \; S^2=S_1\cdot S_2\; \; \Rightarrow \; \; S=\sqrt{S_1S_2}$

5.  

$S(ABCD)=S(ADM)+S(BCM)+S(ABM)+S(DCM)=\\\\=S_1+S_2+2S=S_1+S_2+2\sqrt{S_1S_2}=(\sqrt{S_1}+\sqrt{S_2})^2\\\\S(ABCD)=(\sqrt{S_1}+\sqrt{S_2})^2$