Предмет: Математика,
автор: arkadiysudakov00
Помогите решить плиз.
Приложения:
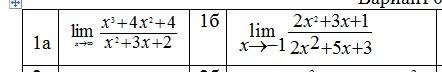
Ответы
Автор ответа:
1
1а)
1б)
arkadiysudakov00:
А по какому принципу решены данные примеры ? Точнее каким методом ?
В первом примере мы просто выносим старшую степень за скобки, в скобках остается единица и сумма бесконечно малых величин, так как икс стремится к бесконечности, и он стоит в знаменателе. Число, деленное на бесконечность - бесконечно малая величина, ей можно пренебречь. То есть в скобках останется просто единица. Сокращая x^3 на x^2 получаем x, который стремится к бесконечности.
Во втором примере выносим (x+1) за скобки в числителе и знаменателе, далее сокращаем их и просто подставляем мину единицу в полученное выражение.
Просто я забыл приписать в задании,точнее в условии,но мне надо решить эти пределы не пользуясь правилом Лопиталя....
Здесь не использовалось правило Лопиталя
Помогите решить другие мои подобные вопросы.я буду вам признателен.)
Похожие вопросы
Предмет: История,
автор: dianatolko
Предмет: История,
автор: tyrloonvip
Предмет: Математика,
автор: fedr9148
Предмет: История,
автор: alevtinatian