Предмет: Алгебра,
автор: um77735
Помогите решить, развёрнуто.
Приложения:
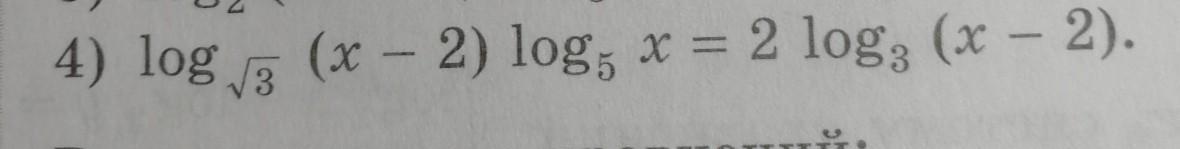
Ответы
Автор ответа:
1
ОДЗ: x є (2;+∞)
1)
Данный корень входит в ОДЗ;
2)
Этот корень тоже входит в ОДЗ.
Ответ: 3, 5.
Автор ответа:
1
Решение во вложении:
Приложения:

um77735:
Почему в начале перед log появляется 2?
корень из 3 это 3 в 1/2 степени, выносим степень 1/1/2=2
Там оснавание логарифма √3, а √3 = 3^1/2, а по свойству логарифма log(a^n)(b) = 1/n * log(a)(b)
Спасибо!
Похожие вопросы
Предмет: История,
автор: chingizd3
Предмет: Қазақ тiлi,
автор: aliya9516
Предмет: Литература,
автор: banan13709090
Предмет: История,
автор: Долума11
Предмет: Алгебра,
автор: MrGraMiHasS