Предмет: Алгебра,
автор: Jemilya
Теория вероятностей,помогите пожалуйста.
Приложения:
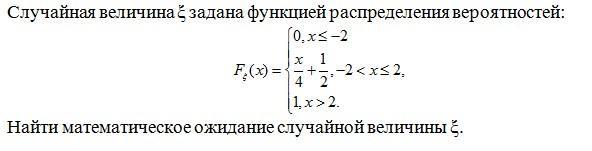
Ответы
Автор ответа:
1
Ответ: M[ξ]=0.
Объяснение:
Исследуя функцию распределения F(x), приходим к выводу, что данная случайная величина распределена только на интервале [2;2]. Находим плотность распределения вероятностей на этом интервале: f(x)=F'(x)=(x/4+1/2)'=1/4, и тогда M[ξ]=∫x*f(x)*dx с пределами интегрирования -2 и 2. Так как ∫x*f(x)*dx=1/4*∫x*dx=1/8*x², то M[ξ]=1/8*2²-1/8*(-2)²=0.
Похожие вопросы
Предмет: География,
автор: ajsigudltekinn
Предмет: ОБЖ,
автор: slimedc
Предмет: Биология,
автор: kolpackovaolga8
Предмет: Литература,
автор: МилкиВэй11