Предмет: Геометрия,
автор: egorovaalina1
Основанием прямого параллелепипеда является ромб с диагоналями 6см и 8см. Диагональ боковой грани равна √61. Определите боковую поверхность призмы.
Ответ с чертежом.
Ответы
Автор ответа:
3
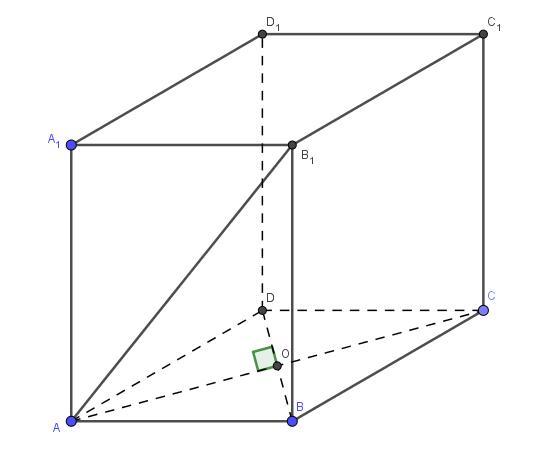
Поскольку основанием параллелепипеда является ромб, то диагонали ромба точкой пересечения делятся пополам и они взаимно перпендикулярны, т.е. AO = OC = AC/2 = 8/2 = 4 см ; OD = OB = 3 см.
Из прямоугольного треугольника AOB по т. Пифагора
см.
AB = BC = CD = AD = 5 см.
По теореме Пифагора из прямоугольного треугольника
см
Площадь боковой поверхности.
Sбок = Росн * h = 4*AB * h = 4 * 5 * 6 = 120 см²
Ответ: 120 см².
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: diana098413
Предмет: Биология,
автор: valentine1816
Предмет: Информатика,
автор: shaburovsasha415
Предмет: Математика,
автор: Sofakh280104Nanachan