Предмет: Алгебра,
автор: nerdynick
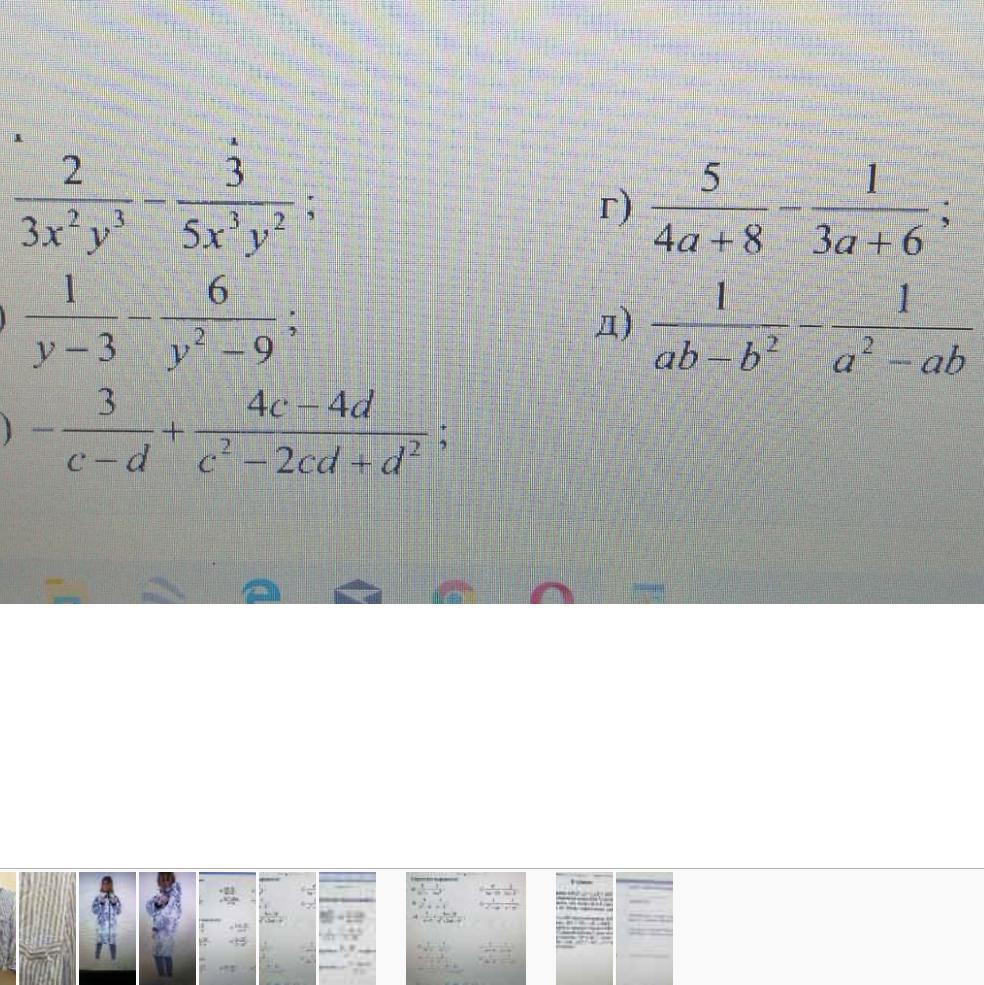
Решите пожалуйста,очень нужно!
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Українська мова,
автор: samosueveo
Предмет: История,
автор: alekseewzheka0207
Предмет: Литература,
автор: sshmrv
Предмет: Математика,
автор: nataliakorotko