Question

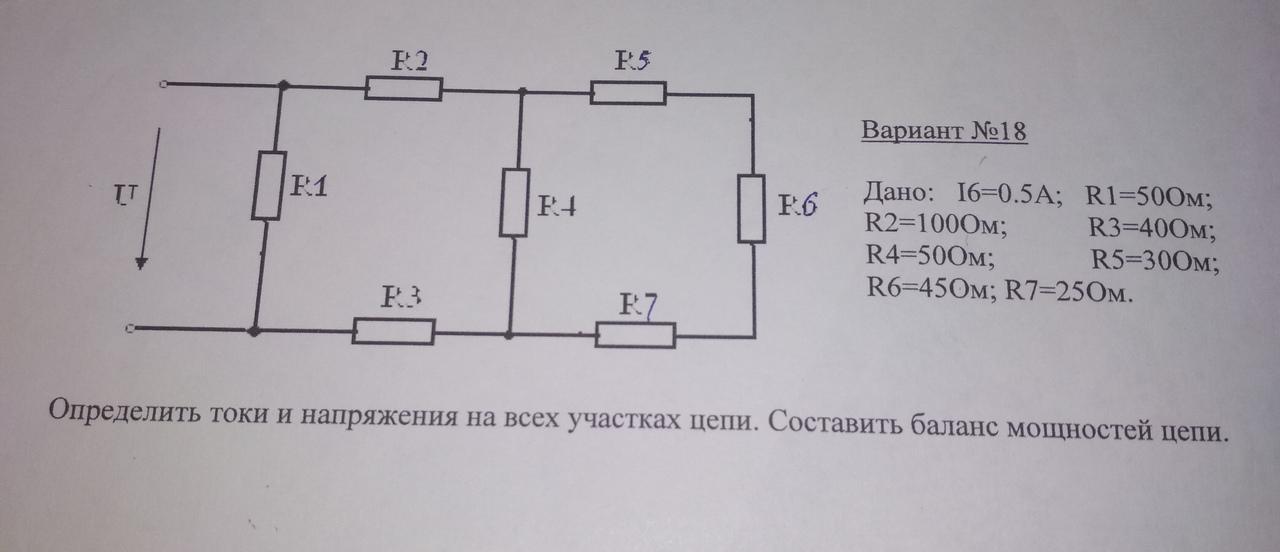
Помогите пожалуйста. Определить токи на всех участках цепи. Составить баланс мощностей цепи.

Answer 1

Ответ:

$U = U_1 = 260$  В ;

$I = 6.7$  А ;

$P = 1742$  Вт ;

$I_1 = 5.2$  А ;

$P_1 = 1352$  Вт ;

$U_2 = 150$  В ;

$I_2 = 1.5$  А ;

$P_2 = 225$  Вт ;

$U_3 = 60$  В ;

$I_3 = 1.5$  А ;

$P_3 = 90$  Вт ;

$U_4 = 50$  В ;

$I_4 = 1$  А ;

$P_4 = 50$  Вт ;

$U_5 = 30$  В ;

$I_5 = 0.5$  А ;

$P_5 = 15$  Вт ;

$U_6 = 22.5$  В ;

$P_6 = 11.25$  Вт ;

$U_7 = 25$  В ;

$I_7 = 0.5$  А ;

$P_7 = 12.5$  Вт.

Объяснение:

Токи через  $R_5$  ,  $R_6$  и  $R_7$  равны, как неразветвляющиеся:  $I_5 = I_7 = I_6 = 0.5$  А ;

Мощности на  $R_5$  ,  $R_6$  и  $R_7$  равны, соответственно:

$P_5 = I_5^2 R_5 = I_6^2 R_5 = 0.5^2 30$  Вт  $= 7.5$  Вт ;

$P_6 = I_6^2 R_6 = 0.5^2 450$  Вт  $= 11.25$  Вт ;

$P_7 = I_7^2 R_7 = I_6^2 R_7 = 0.5^2 250$  Вт  $= 6.25$  Вт ;

Напряжения на  $R_5$  ,  $R_6$  и  $R_7$  равны, соответственно:

$U_5 = I_5 R_5 = I_6 R_5 = 0.5 \cdot 30$  В  $= 15$  В ;

$U_6 = I_6 R_6 = 0.5 \cdot 45$  В  $= 22.5$  В ;

$U_7 = I_7 R_7 = I_6 R_7 = 0.5 \cdot 25$  В  $= 12.5$  В ;

Общее напряжение на  $R4$  и участке, состоящем из  $R_5$  ,  $R_6$  и  $R_7$  равны, как параллельно подключённые:

$U_4 = U_5 + U_6 + U_7 = I_6 ( R_5 + R_6 + R_7 ) = 0.5 ( 30 + 45 + 25 )$  В  $=$

$= 0.5 \cdot 100$  В  $= 50$  В ;

Мощность на  $R_4$  равна:

$P_4 = \frac{U_4^2}{R_4} = \frac{I_6^2}{R_4} ( R_5 + R_6 + R_7 )^2 = \frac{0.5^2}{50} ( 30 + 45 + 25 )^2$  Вт  $= 50$  Вт ;

Ток через  $R_4$  по закону Ома:

$I_4 = \frac{ U_4 }{ R_4 } = I_6 \cdot \frac{ R_5 + R_6 + R_7 }{ R_4 } = 0.5 \cdot \frac{ 30 + 45 + 25 }{ 50 }$  А  $= 1$  А ;

Токи через  $R_2$  и  $R_3$  , как, соответственно, разветвляющийся и стекающийся, находятся суммированием токов через  $R_4$  и через участок, состоящий из  $R_5$  ,  $R_6$  и  $R_7$  :

$I_2 = I_3 = I_4 + I_6 = I_6 ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) = 0.5 ( 1 + \frac{ 30 + 45 + 25 }{ 50 } )$  А  $= 1.5$  А ;

Мощности на  $R_2$  и  $R_3$  равны, соответственно:

$P_2 = I_2^2 R_2 = ( I_6 ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) )^2 R_2 = ( 0.5 ( 1 + \frac{ 30 + 45 + 25 }{ 50 } ) )^2 100$  Вт  $=$

$= 225$  Вт ;

$P_3 = I_3^2 R_3 = ( I_6 ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) )^2 R_3 = ( 0.5 ( 1 + \frac{ 30 + 45 + 25 }{ 50 } ) )^2 100$  Вт  $=$

$= 90$  Вт ;

Напряжения на  $R_2$  и  $R_3$  равны, соответственно:

$U_2 = I_2 R_2 = I_6 ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) R_2 = 0.5 ( 1 + \frac{ 30 + 45 + 25 }{ 50 } ) 100$  В  $= 150$  В ;

$U_3 = I_3 R_3 = I_6 ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) R_3 = 0.5 ( 1 + \frac{ 30 + 45 + 25 }{ 50 } ) 40$  В  $= 60$  В ;

Общее напряжение на  $R_1$  и участке, состоящем из  $R_2$  ,  $R_3$  и  $R_4$  (с распараллеливанием) равны, как параллельно подключённые:

$U = U_1 = U_2 + U_4 + U_3 = I_2 R_2 = I_6 ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) ( R_2 + R_3 ) + I_6 ( R_5 + R_6 + R_7 ) =$

$= I_6 ( ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) ( R_2 + R_3 ) + R_5 + R_6 + R_7 ) =$

$= 0.5 ( ( 1 + \frac{ 30 + 45 + 25 }{ 50 } ) ( 100 + 40 ) + 30 + 45 + 25 )$  В  $= 260$  В ;

Мощность на  $R_1$  равна:

$P_1 = \frac{ U_1^2 }{ R_1 } = \frac{ I_6^2 }{ R_1 } ( ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) ( R_2 + R_3 ) + R_5 + R_6 + R_7 )^2 =$

$= \frac{ 0.5^2 }{ 50 } ( ( 1 + \frac{ 30 + 45 + 25 }{ 50 } ) ( 100 + 40 ) + 30 + 45 + 25 )^2$  Вт  $= 1352$  Вт ;

Ток через  $R_1$  по закону Ома:

$I_1 = \frac{ U_1 }{ R_1 } = \frac{ I_6 }{ R_1 } ( ( 1 + \frac{ R_5 + R_6 + R_7 }{ R_4 } ) ( R_2 + R_3 ) + R_5 + R_6 + R_7 ) =$

$= \frac{ 0.5 }{ 50 } ( ( 1 + \frac{ 30 + 45 + 25 }{ 50 } ) ( 100 + 40 ) + 30 + 45 + 25 )$  А  $= 5.2$  А ;

Общий ток, как разветвляющийся:

$I = I_1 + I_3 = ( 5.2 + 1.5 )$  А  $= 6.7$  А  $= 6.7$  А ;

Общая мощность:

$P = UI = 260 \cdot 6.7$  Вт  $= 26 \cdot 67$  Вт  $= 1742$  Вт ;

Баланс мощности:

$P_1 + P_2 + P_3 + P_4 + P_5 + P_6 + P_7 = P$  ;

$1352 + 225 + 90 + 50 + 7.5 + 11.25 + 6.25 = 1352 + 225 + 140 + 7.5 + 17.5 = 1492 + 225 + 25 = 1492 + 250 = 1742$  .