Помогите с интегралом пожалуйста, как его решить с помощью замены cos²x=t?
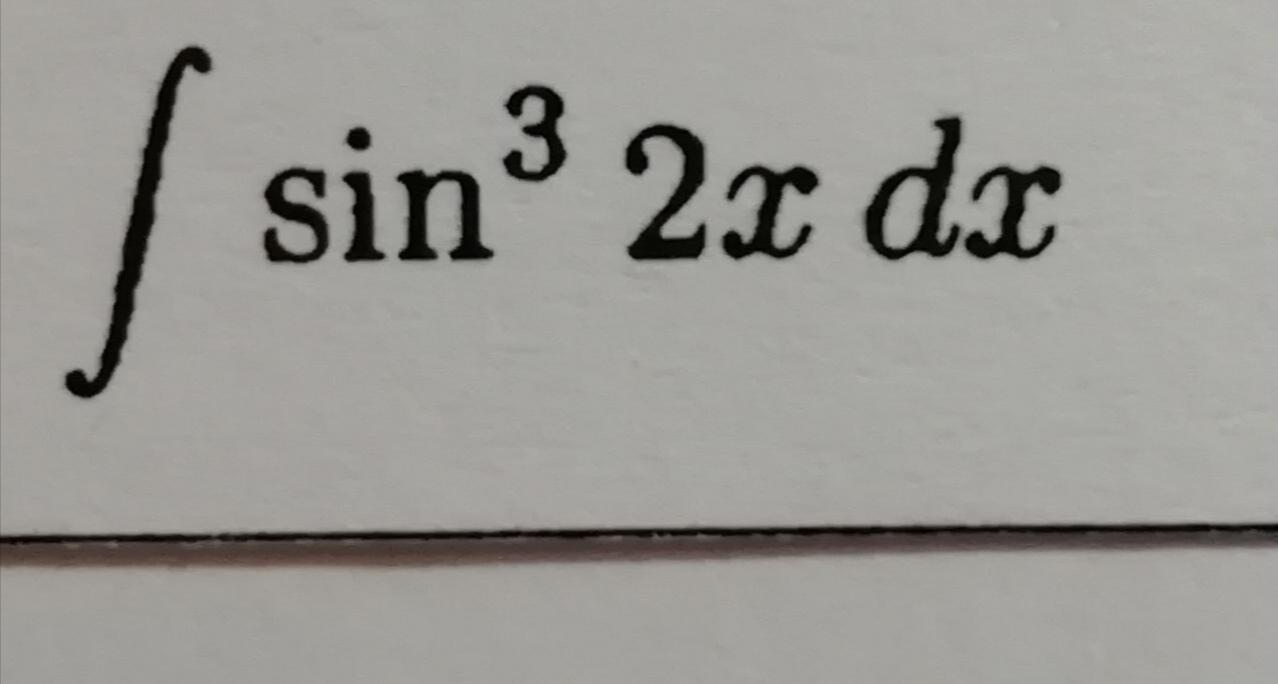
Ответы
Ответ:
∫
sin
3
(
2
x
)
d
x
Пусть
u
1
=
2
x
. Тогда
d
u
1
=
2
d
x
, следовательно
1
2
d
u
1
=
d
x
. Переписать, используя
u
1
и
d
u
1
.
∫
sin
3
(
u
1
)
1
2
d
u
1
Обьединяем
sin
3
(
u
1
)
и
1
2
.
∫
sin
3
(
u
1
)
2
d
u
1
Поскольку
1
2
является константой по отношению к
u
1
, вынесем
1
2
из интеграла.
1
2
∫
sin
3
(
u
1
)
d
u
1
Выносим за скобки
sin
2
(
u
1
)
.
1
2
∫
sin
2
(
u
1
)
sin
(
u
1
)
d
u
1
Используя формулу Пифагора, запишем
sin
2
(
u
1
)
в виде
1−cos2(u1) 12∫(1−cos2(u1))sin(u1)du1
Пусть u2=cos(u1)
Тогда du2=−sin(u1)du1
следовательно
−1sin(u1)du2=du1
Переписать, используя u2
и du2.
12∫−1+u22du2
Разложим интеграл на несколько интегралов.
12(∫−1du2+∫u22du2)
Поскольку
−1
является константой по отношению к
u2
, вынесем
−1
из интеграла.
12(−u2+C+∫u22du2)
По правилу дифференцирования функции, интегралом от
u22
относительно
u2
является 13u23.12(−u2+C+13u23+C)
Упростим.
12(−u2+13u23)+C
12(−cos(2x)+13cos3(2x))+C
Упростим ответ.
−cos(2x)2+cos3(2x)6+C
Изменим порядок членов.−12cos(2x)+16cos3(2x)+C