Предмет: Математика,
автор: artalex74
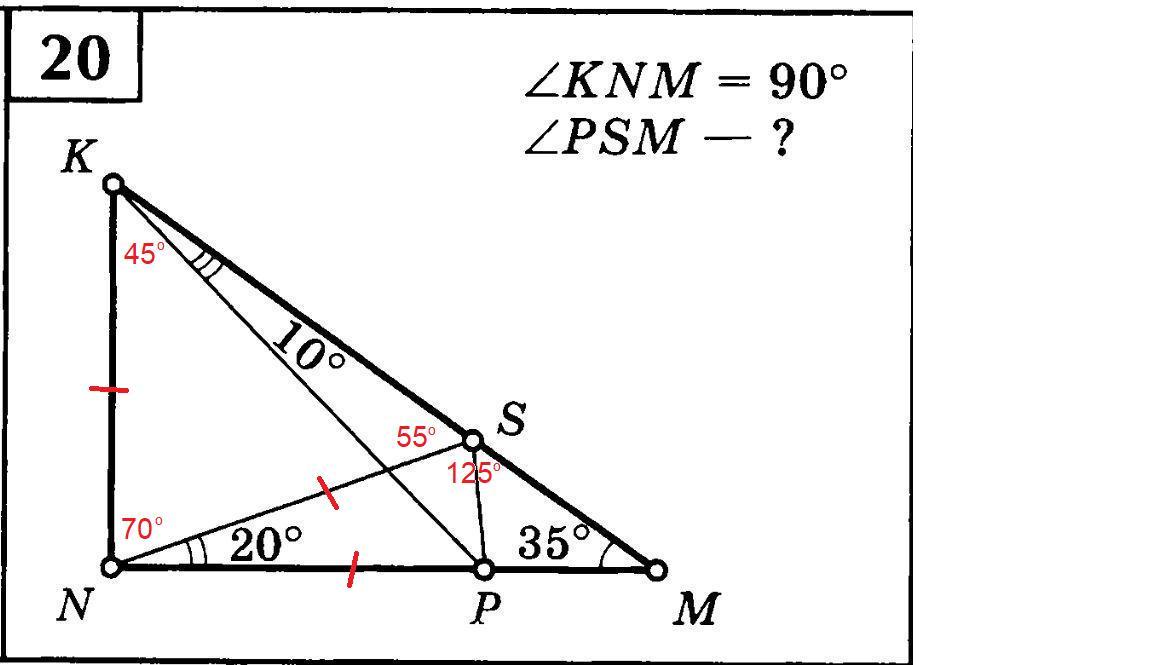
Геометрия. Условие задачи на фото.
Приложения:

Аноним:
45
Ответы
Автор ответа:
5
Ответ: 45°
Пошаговое объяснение:
ΔNSM: ∠NSM = 180° - (∠SNM + ∠SMN) = 180° - (20° + 35°) = 180° - 55° =
= 125°
∠NSK = 20° + 35° = 55°, как внешний угол ΔNSM (или можно найти как смежный с ∠NSM)
∠KNS = 90° - 20° = 70°
ΔKNS: ∠NKS = 180° - (∠KNS + ∠NSK) = 180° - (70° + 55°) = 180° - 125° = 55°
Итак, в треугольнике KNS два угла по 55°, следовательно он равнобедренный с основанием KS,
NK = NS
∠NKP = 55° - 10° = 45°
ΔNKP прямоугольный, с углом 45°, значит он равнобедренный,
NK = NP.
Итак, NK = NS и NK = NP, значит NS = NP, т.е.
ΔNSP равнобедренный. Найдем в нем углы при основании:
∠NSP = ∠NPS = (180° - 20°) / 2 = 160° / 2 = 80°
∠PSM = ∠NSM - ∠NSP = 125° - 80° = 45°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: bahytkalievbagzan
Предмет: Українська література,
автор: babandry
Предмет: Геометрия,
автор: nubovicnub3
Предмет: Физика,
автор: Devil1d
Предмет: Математика,
автор: Яна181111