Можно с решением пожалуйста.
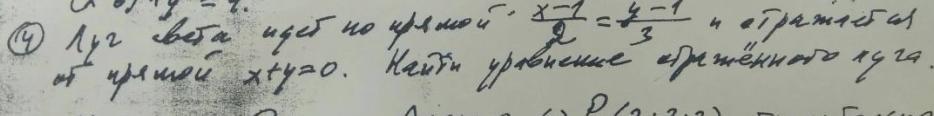
Ответы
Даны прямы: 1) (х - 1)/2 = (у -1)/3, 2) х + у = 0.
Преобразуем их в уравнения с угловым коэффициентом.
1) (х - 1)/2 = (у -1)/3, 3х - 3 = 2у - 2, у = (3/2)х - (1/2).
2) у = -х.
Находим точку М - точку пересечения заданных прямых.
(3/2)х - (1/2) = -х,
(5/2)х = 1/2,
х = 1/5, у = -х = -1/5. Точка М((1/5); (-1/5)).
Определяем уравнение перпендикуляра из точки М к прямой 2).
к(М) = -1/к(2) = -1/-1 = 1.
Уравнение перпендикуляра из точки М к прямой 2) имеет вид:
у = 1*х + в. Для определения в подставим координаты точки М.
-1/5 = (1/5)*1 + в, в = -2/5. Уравнение перпендикуляра у = х - (2/5).
Это прямая 3).
Находим тангенс угла между прямыми 1) и 3) по их угловым коэффициентам: к(1) = (3/2), к(2) = 1.
tg a = (1,5 - 1)/(1 + 1,5*1) = 0,5/2,5 = 1/5.
Отражённый луч идёт по прямой 4), симметричной прямой 1) относительно 3). Примем угловой коэффициент прямой 4) = х.
tg b = 1/5 = (1 -x) /(1 + 1*x),
1 + x = 5 - 5x,
6x = 4. х= 4/6 = 2/3.
Уравнение 4): у =(2/3)х + в. Подставим М:
-1/5 = (2/3)*(1/5) + в, в = (-1/5) - (2/15) = -5/15 = -1/3.
Ответ: уравнение 4) у = (2/3)х - (1/3).
