Предмет: Алгебра,
автор: gyvyh
Логарифмические уравнения. Решите пожалуйста на листочке подробно.
Приложения:
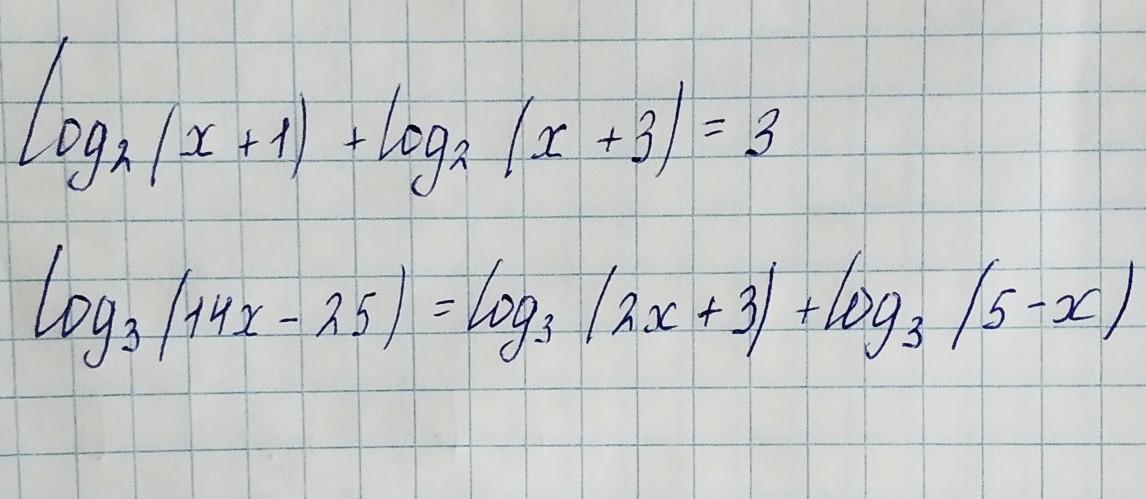
Universalka:
Могу решить, но не на листочке
хорошо
Ответы
Автор ответа:
1
1) ОДЗ :
2) ОДЗ :
14x - 25 > 0 ⇒ x > 1 11/14
2x+3 > 0 ⇒ x > - 1,5
5 - x > 0 ⇒ x < 5
Окончательно : x ∈ (1 11/14 ; 5)
Похожие вопросы
Предмет: Алгебра,
автор: rymbekarsen
Предмет: Литература,
автор: nikjoy30
Предмет: Алгебра,
автор: vladzuev2020
Предмет: Математика,
автор: annasukhova2014