Предмет: Алгебра,
автор: aidhelld1
Помогите решить 3 задания 1)|2x+1|-|3-2|,если x принадлежит (1 1/10,+ бесконечность)
Приложения:
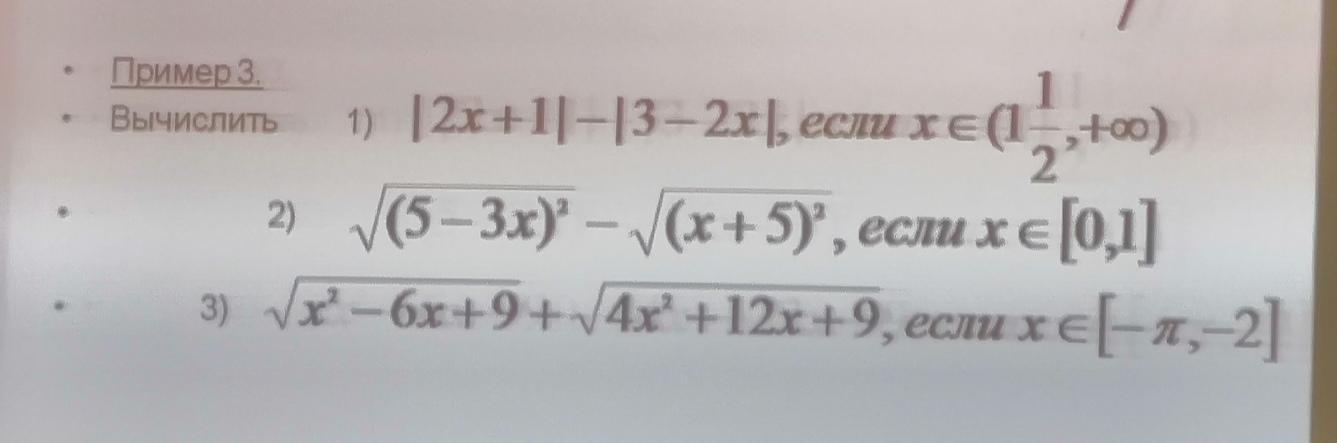
mmb1:
все три ?
Да
Ответы
Автор ответа:
3
|a| = a a>=0
= -a a<0
1/
|2x + 1| - |3 - 2x|
x∈ (3/2 +∞)
подмодульные выражения первое положительно второе отрицательно, второе открывается 2х-3
2x + 1 - (2x - 3) = 2x + 1 - 2x - 3 = -2
2/
√(5 - 3x)² - √(x + 5)² = |5 - 3x| - |x + 5| на интервале х∈[0, 1]
оба подмодульных выражения положительны
5 - 3х - x - 5 = -4x
3/
√(x² - 6x + 9) + √(4x² + 12x + 9) = √(x - 3)² + √(2x + 3)² = |x - 3|+|2x+3|
x∈[-π, -2] ≈ [-3.14, -2 ]
на этом интерале оба подмодульгых выражения отрицательны значит отурываются как 3-х и -2х-3
3 - х - 2х - 3 = -3х
Спасибо за быстрый ответ после проверки оценю
так вы посмотрите что такое модуль и как они раскрываются, и сами повторите решение
ничего трудного пока нет ....
посмотреть подмодульное выражение и раскрыть его с плюсом или минусом
ничего трудного пока нет ....
посмотреть подмодульное выражение и раскрыть его с плюсом или минусом
Похожие вопросы
Предмет: Русский язык,
автор: asiya2602dr
Предмет: Информатика,
автор: nicknicknicknick77
Предмет: Математика,
автор: bannikivegor6
Предмет: Алгебра,
автор: sknt
Предмет: Математика,
автор: Voin7777