Предмет: Алгебра,
автор: vanserebro
Помогите с решением, ребят, баллами не обижу.
Приложения:
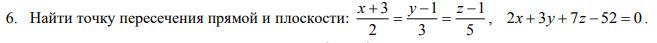
Ответы
Автор ответа:
2
Представим наше уравнение прямой в параметрической форме
Подставляем в уравнение плоскости
Значит, точки пересечения данной прямой и плоскости:
Ответ: (-1;4;6).
Автор ответа:
0
Ответ: точка пересечения прямой и плоскости (-1;4;6)
Объяснение во вложении
Приложения:

Похожие вопросы
Предмет: Математика,
автор: tarasenkovnikita286
Предмет: Алгебра,
автор: MMMMmmmmmmk
Предмет: Алгебра,
автор: kyvver
Предмет: Математика,
автор: zhaksylykaytzh
Предмет: История,
автор: ganter122333
https://znanija.com/task/33163431