Прошу, выручите с решение задания по функциям, буду неимоверно благодарен каждому!
Исследуйте функцию и постройте её график с помощью производной по данной схеме исследования:
1) D(y)
2) Нули функции;
3) Чётность/нечётность, симметричность графика;
4) Точки разрыва, монотонность;
5) Промежутки возр./убыв.;
6) Промежутки выпуклости;
7) График;
8) Дополнительные точки.
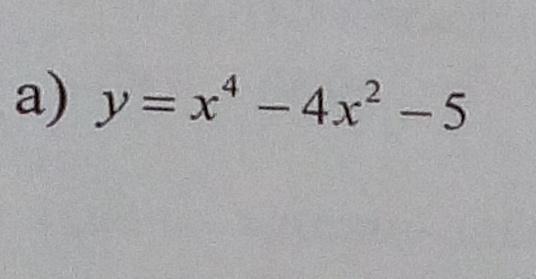
Ответы
Пошаговое объяснение:
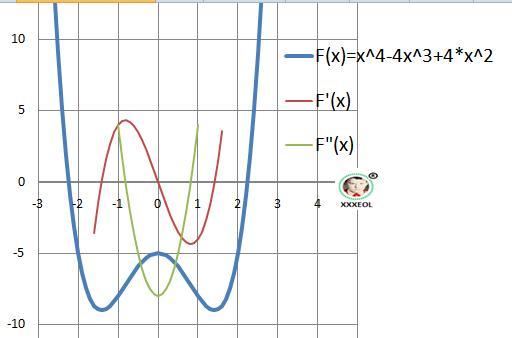
Уравнение четвертой степени с положительным коэффициентом - "коренной зуб".
Рисунок с графиком функции в приложении.
1. Область определения функции. Непрерывная. Разрывов нет.
D(y) = (-∞;+∞)
2. Корни функции: х₁ = -√5 и х₃ = √5. Двух других нет. Нахождение самих корней - без комментариев.
3. Интервалы знакопостоянства.
Положительна: Y>0 X∈(-∞;-√5)∪(0.52;+∞) - вне корней.
Отрицательна: Y<0 X∈(-√5;√5) - между корней.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 4*x³ -8*x = 4x*(x² -2) = 0
Точки экстремумов: x₅ = - √2, x₆ = √2, x₇ = 0
5 Локальные экстремумы: Ymin(√2) = Y(-1,44) = - 9 , Ymax(0) = -5
6. Интервалы монотонности.
Убывает: Х∈(-∞;-√2)∪(0;√2)
Возрастает: Х∈(-√2;0)∪(√2;+∞)
7, Поиск точек перегиба по второй производной
Y"(x) = 12*x² -8 = = 0
x₈ = - √6/3 и х₉ = √6/3 ( 0,82)- точки перегиба.
8. Вогнутая - "ложка" - Х∈(-∞;-0,82)∪(х9=0,82;+∞) - вне корней.
Выпуклая - "горка" - Х∈(-0,82;(0,82))
График на рисунке в приложении.