Предмет: Геометрия,
автор: kristina13mezha
Даны окружность, заданная уравнением х^2 + у^2 − 2у − 8 = 0, и точка А (4; 4). Напишите уравнение окружности, имеющей центр в данной точке и касающейся данной окружности внешним образом.
Ответы
Автор ответа:
2
Даны окружность х^2 + у^2 − 2у − 8 = 0 и точка А (4; 4).
Выделим полные квадраты х^2 + у^2 − 2у − 8 = х^2 + у^2 − 2у + 1− 9 =
= х^2 + (у - 1)^2 = 9.
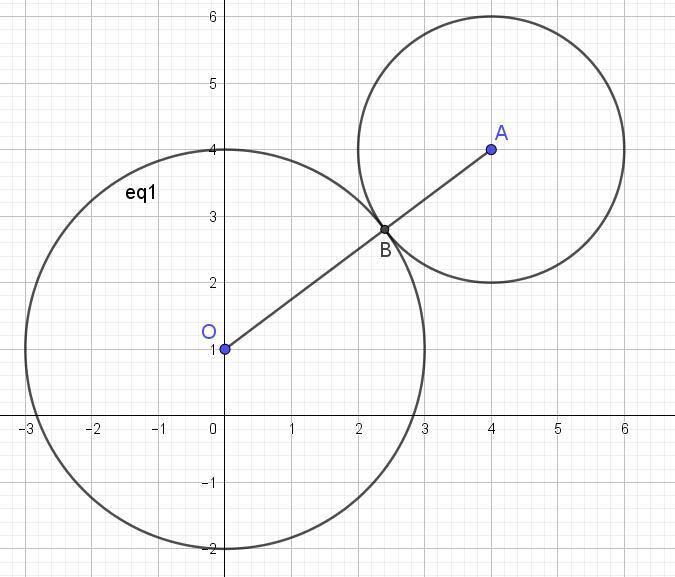
Это окружность с центром в точке О(0; 1) и радиусом 3.
Отрезок ОА как сумма радиусов окружностей (заданной и искомой) равен: ОА = √((4 - 0)² + (4 - 1)²) = √(16 + 9) = √25 = 5.
Тогда радиус искомой окружности равен 5 - 3 = 2.
Ответ: (х - 4)² + (у - 4)² = 2².
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: pupil2017d10
Предмет: Английский язык,
автор: sofia123357
Предмет: Химия,
автор: omasempai
Предмет: Математика,
автор: ann446