Предмет: Алгебра,
автор: МаргэретТЭччерр
1. Решить систему уравнений методом подстановки:
а) x+y=3,
y ² - xy = -1 ;
б) 1/х + 1/у =3/4,
х-у=2 .
2.. Решить систему уравнений методом алгебраического сложения:
2х² + 3у²=14,
-х² + 2у² = 7.
Ответы
Автор ответа:
0
Решение во вложении.......................
Приложения:
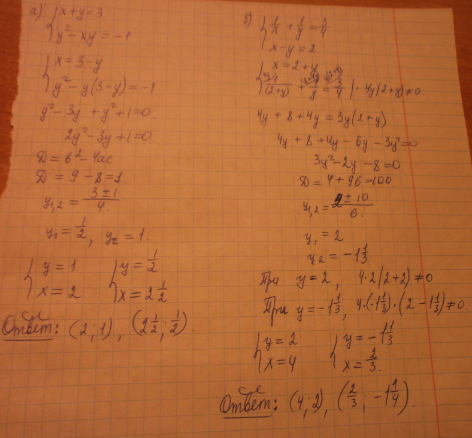
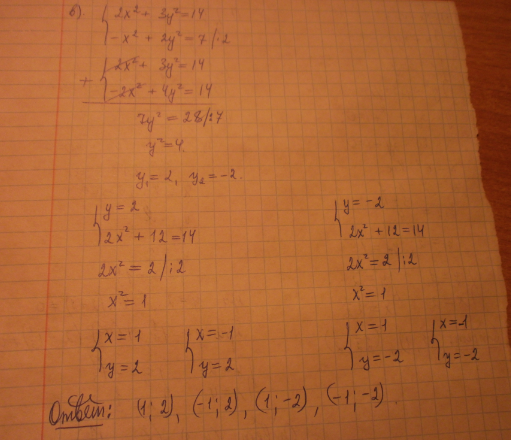
Автор ответа:
0
1.
а)

Ответ:
б)

Ответ:
2.

Ответ:
а)
Ответ:
б)
Ответ:
2.
Ответ:
Приложения:
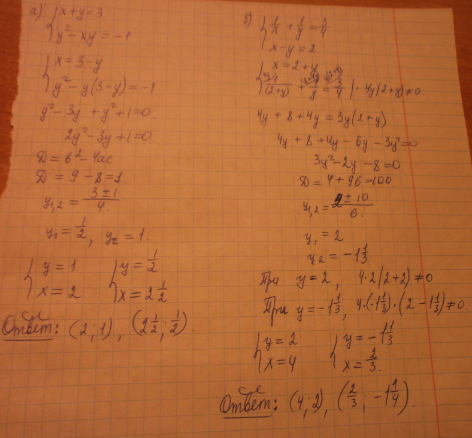
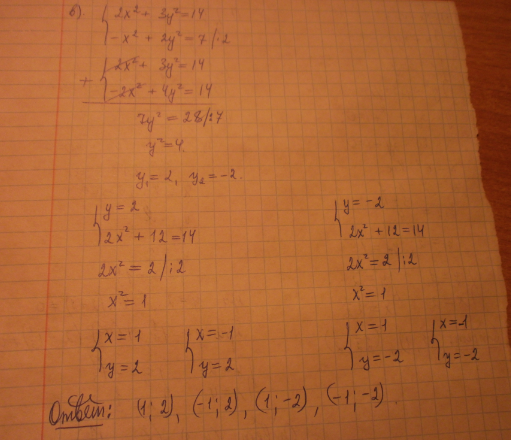
Похожие вопросы
Предмет: Алгебра,
автор: meol1nk
Предмет: География,
автор: angelina4880
Предмет: Другие предметы,
автор: S0rux
Предмет: Химия,
автор: Patriot009