Предмет: Алгебра,
автор: cdsgdgsjhn
Помогите, пж пж пж! ОЧЕНЬ нужно!!!!!!
Докажите тождество при a не равно +-1:

Приложения:
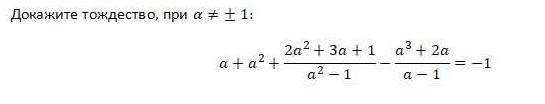
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Українська мова,
автор: Smechariki67
Предмет: Литература,
автор: klimovzaharchik
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Likoris
Предмет: Математика,
автор: умныйнеглупый