Предмет: Алгебра,
автор: dasha240324
Решите уравнение пожалуйста)
Приложения:
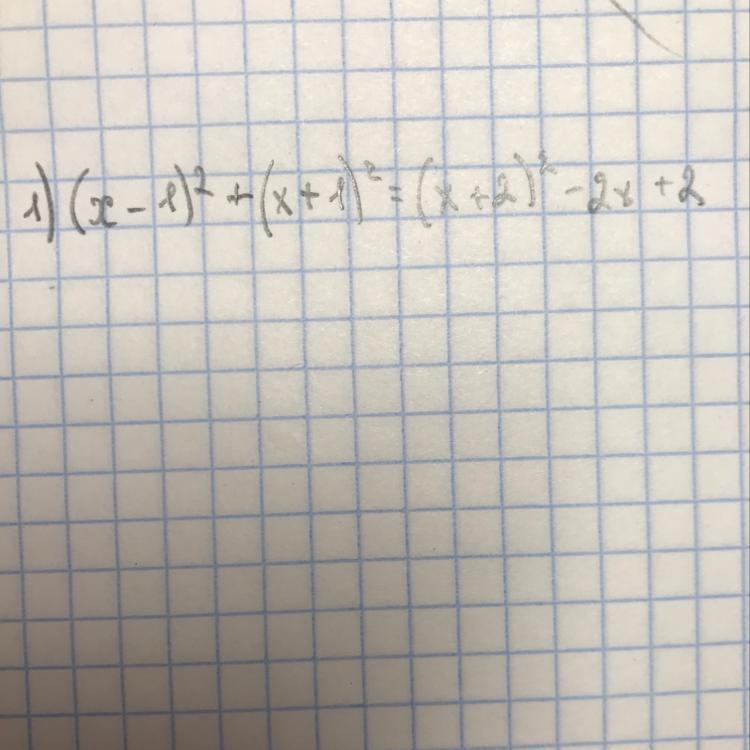
Ответы
Автор ответа:
2
Ответ:
,
Решение:
Преобразуем исходное выражение:
По формулам сокращенного умножения имеем:
Упростим выражение:
Перенесем все в левую часть:
Решим уравнение:
Похожие вопросы
Предмет: Математика,
автор: MgPokemon
Предмет: Русский язык,
автор: renatmm85
Предмет: Химия,
автор: siposoru
Предмет: Математика,
автор: милаяласточка
Предмет: Биология,
автор: shelest03