Question

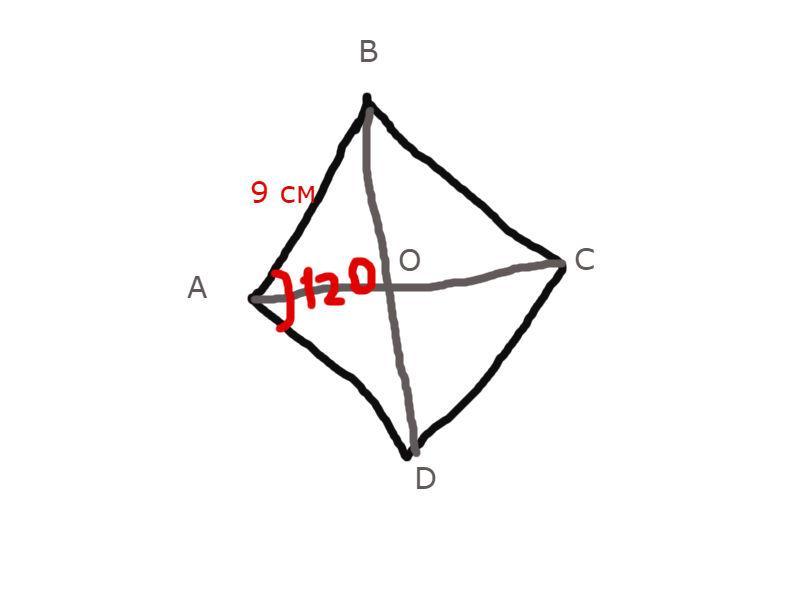
один из углов ромба равен 120 Сторона ромба ровна 9 см. найдите меньшую диагональ ромба ​

Answer 1

Ответ:

9 см

Объяснение:

1) Рассмотрим ΔАВО

∠А пополам делит биссектриса АС ⇒ ∠ВАС = ∠А : 2 и ∠ВАС = ∠САD

∠ВАС = 120 : 2 = 60°

∠АОB = 90° (т.к. в ромбе биссектрисы перпендикулярны)

и чтобы найти ∠АВО = 180°- ∠ВОА - ∠ВАО (по теореме о сумме углов треугольника)

∠АВО = 180° - 60° - 90° = 30°

2) Катет, лежащий против угла, величина которого равна 30°, равен половине гипотенузы. В ΔАВО, АВ - гипотенуза, равная 9 см, а АО - катет, лежащий против угла 30°. Следовательно, АО = 9:2 = 4,5 см

3) Ромб является параллелограммом, а мы знаем, что в параллелограмме, диагонали точкой пересечения делятся пополам ⇒ АС = АО + ОС и АО = ОС = 4,5

АС = 4,5 + 4,5 = 9 см