Предмет: Алгебра,
автор: Ebaha
Комплексные числа. Найти действительные решения уравнения. Не пойму что дальше делать
Приложения:

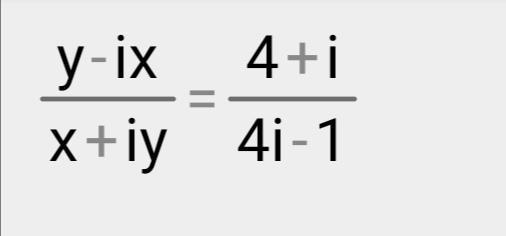
Ответы
Автор ответа:
2
По пропорции : и раскроем скобки
Приравниваем действительные и мнимые частей уравнения
Значения х,у - любые, кроме 0, поскольку левая часть исходного равенства при х = у = 0 не определён.
Похожие вопросы
Предмет: Литература,
автор: matveypanche
Предмет: Геометрия,
автор: svetaisuk1
Предмет: Українська мова,
автор: aleks07master
Предмет: История,
автор: Гарбуз1а
Предмет: Информатика,
автор: awiseman00