Предмет: Геометрия,
автор: flicksho2
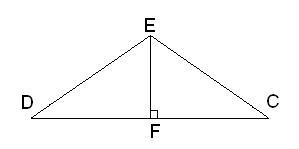
35 Баллов. EC=DE,∢DEC=141°. Найти угол FCE.
Приложения:
Ответы
Автор ответа:
7
Дано :
,
.
.
Найти :
Решение :
- Сумма внутренних углов треугольника равна
.
Тогда -
Так как (по условию), то
- равнобедренный (по определению).
- Углы равнобедренного треугольника при основании равны.
Тогда
Ответ :
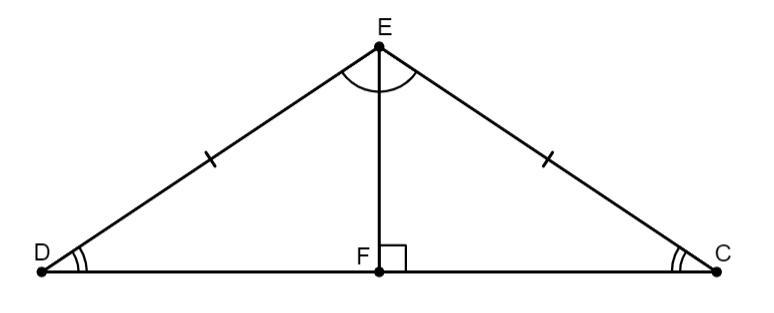
Приложения:
Похожие вопросы
Предмет: Литература,
автор: tsarovapolina2312
Предмет: Математика,
автор: molevnikita31
Предмет: Обществознание,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: Lilianna2504