Предмет: Алгебра,
автор: anna17196
Решите пожалуйста дифференциальное уравнение
Приложения:
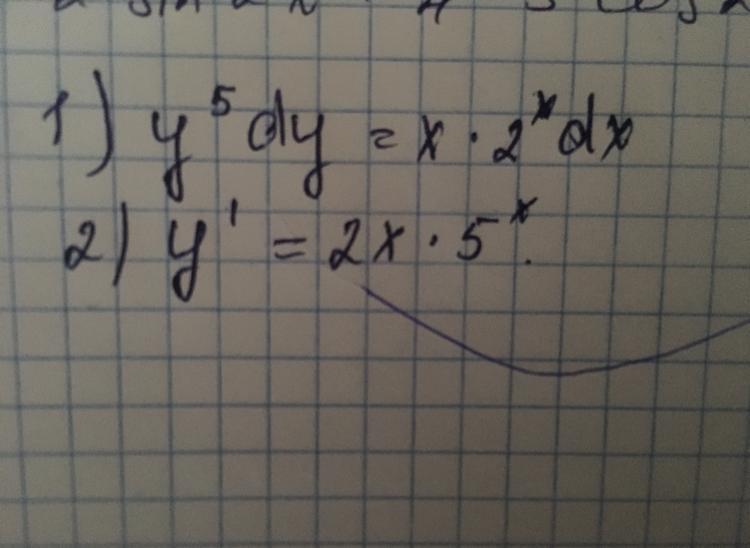
Ответы
Автор ответа:
1
1) Данное дифференциальное уравнение сведён к уравнению с разделёнными переменными. Проинтегрируем обе части уравнения
В правой части уравнения решим интеграл по частям
Получаем — общий интеграл.
2) Здесь дифференциальное уравнение с разделяющимися переменными.
Снова же в правой часть уравнения решим интеграл по частям
Получаем — общее решение.
Похожие вопросы
Предмет: Українська література,
автор: misterartem3000
Предмет: Химия,
автор: Tiktokeer134
Предмет: Английский язык,
автор: uzhetkergenkyzy
Предмет: Физика,
автор: Ятсан888
Предмет: Химия,
автор: anastasiyakozl3