Question

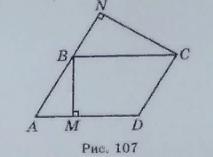
В параллелограмме ABCD проведены высоты BM и CN. Докажите подобие треугольников ABM u BCN.

Answer 1

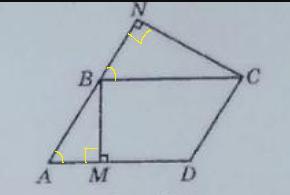
Дано : ABCD - параллелограмм, BM⊥AD, CN⊥AB

Доказать : ΔABM ~ ΔBCN

Доказательство :

AD║BC,  BM⊥AD  ⇒  BM⊥BC  ⇒  ∠MBC = 90°

Δ ABM - прямоугольный. Сумма острых углов прямоугольного треугольника равна 90°

∠ABM = 90° - ∠A

∠ABN = 180°   -   развёрнутый

∠ABN = ∠ABM + ∠MBC + ∠CBN

 180° = (90° - ∠A) + 90° + ∠CBN

 180° = 180° - ∠A + ∠CBN

 ∠CBN = ∠A

Прямоугольные треугольники  ΔABM  и  ΔBCN подобны по равному острому углу.

$\boxed{\boldsymbol{\triangle ABM \thicksim \triangle BCN}}\ \ \ \blacksquare$