Предмет: Алгебра,
автор: CHudesnayaLedi
Помогите пожалуйста с решением

(sin п/3)^2х-2 =2/4
Ответы
Автор ответа:
2
Автор ответа:
0
Ответ: во вложении Объяснение:
Приложения:
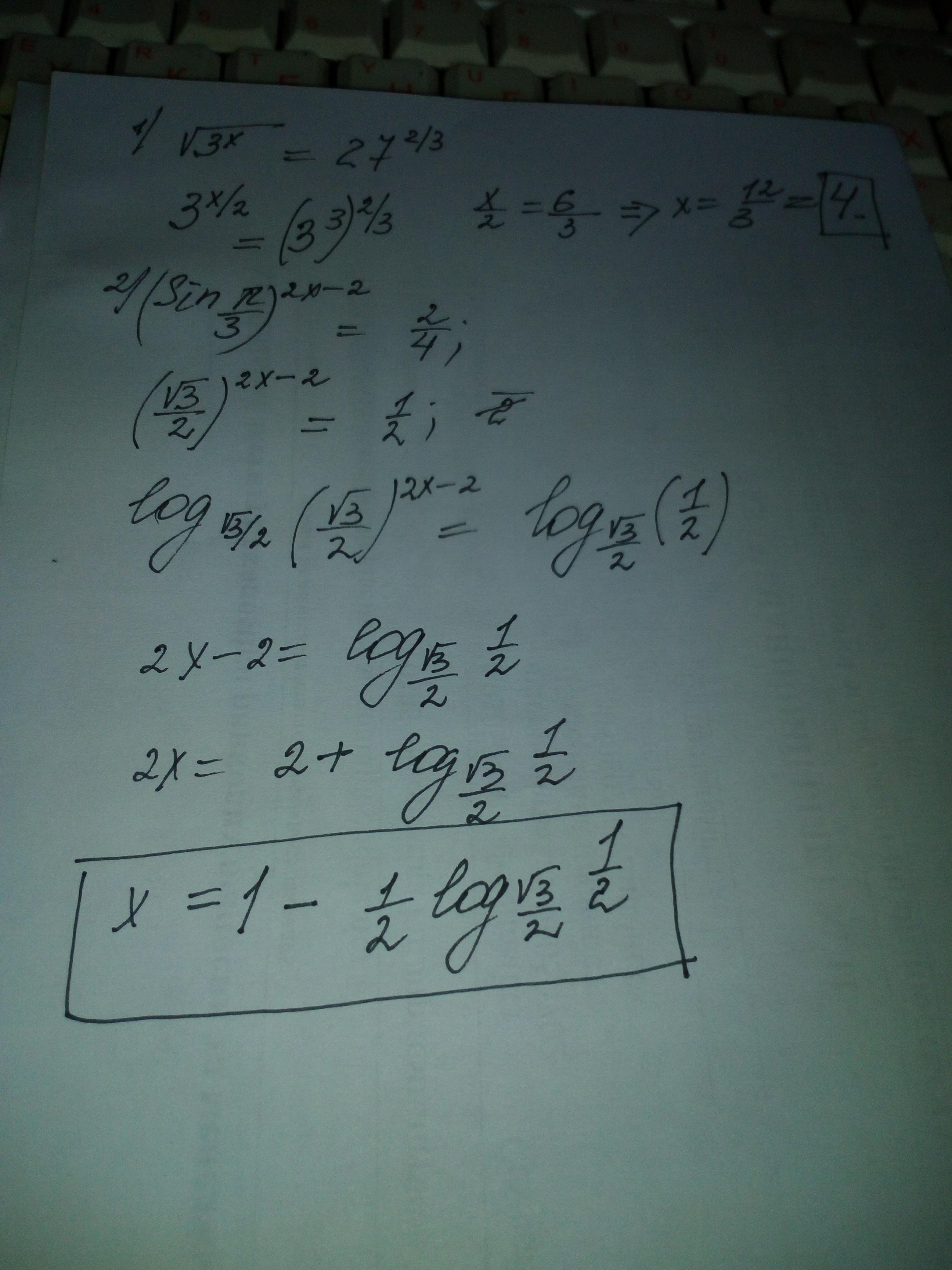
NNNLLL54:
основание задано не sin П/6 , а sinП/3 .
и в 1 примере ошибка
Похожие вопросы
Предмет: Математика,
автор: lerapalagnuk59
Предмет: Математика,
автор: goker3981
Предмет: Русский язык,
автор: maxtes6664
Предмет: Литература,
автор: JuliaReshet
Предмет: Математика,
автор: даниелла3