Решите, пожалуйста очень нужно!
Заранее спасибо)


Ответы
Ответ:
.........................


Ответ:
11. 30°
12. 30°
13. 124°
14. 36°
15. 83°
16. 110°
17. 36°
18. 38°
19. 68°
20. 36
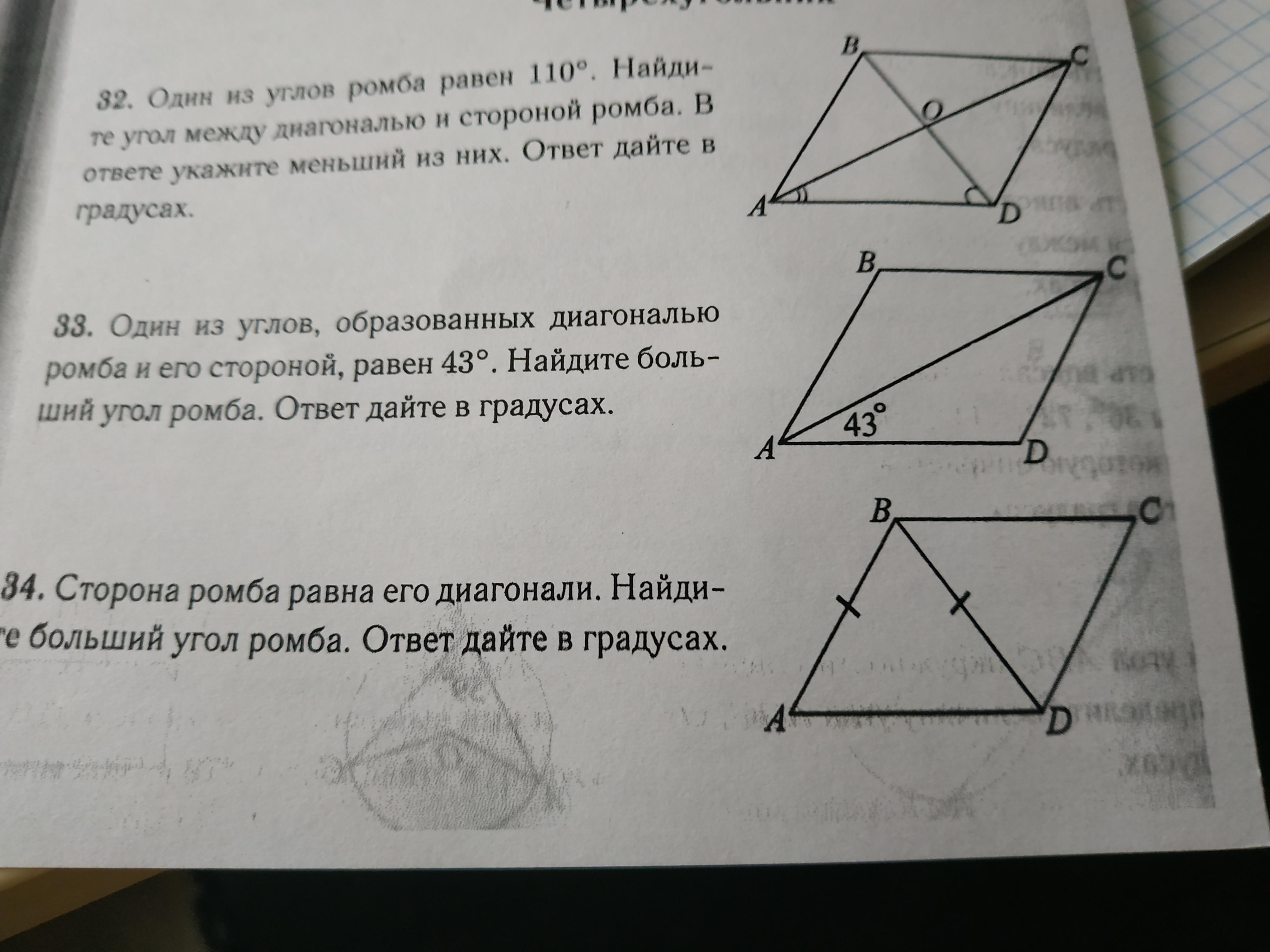
32. 35°
33. 94°
34. 120°
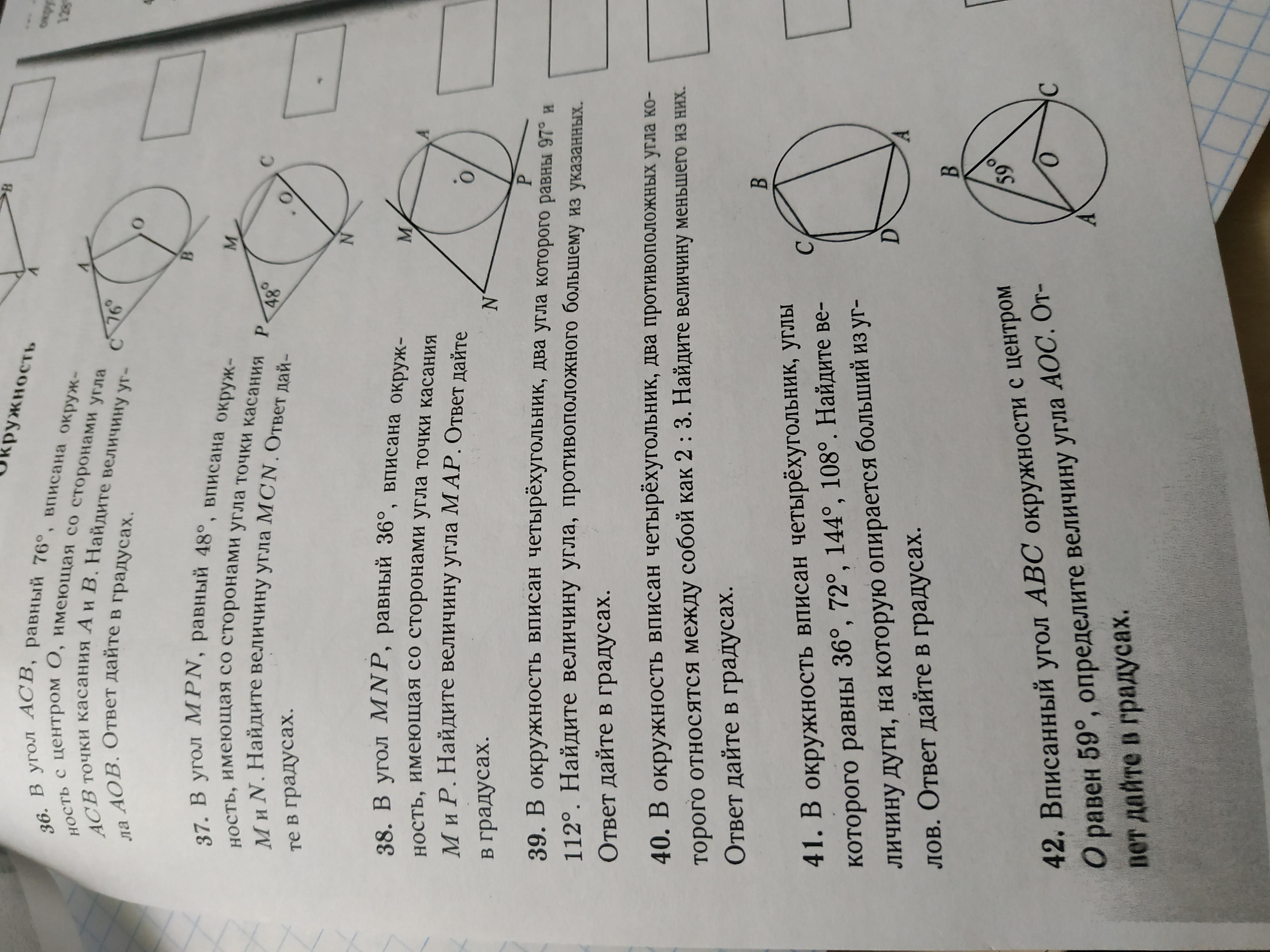
36. 104°
37. 66°
38. 72°
39. 68°
40. 72°
41. 288°
42. 118°
Объяснение:
11.
∡ABC= 30° т.к. по обратному свойству углов прямоугольного треугольника, против, катета равному половине гипотенузы, лежит угол в 30 градусов.
12.
Меньший угол будет равен 30° т.к. мы получаем 2 треугольника тупоугольный(где угол в 105°) и остроугольный. у нас известно что это биссектриса, значит она делит угол в 90° пополам, т.е. углы будут по 45°.
Рассмотрим тупоугольный треугольник.
Сумма углов треугольника 180 => меньший угол будет равен 180-45-105=30°
13.
Внешний угол равен сумме 2-х других углов этого треугольника.
Сначала найдет углы при основании: (180-68):2=56°.
Дальше складываем угол при основании и угол в 68° =>
Внешний угол равен: 56+68=124°
14.
В треугольнике сумма углов равна 180°
Запишем это для треугольника АВС
∠А+∠В+∠С=180°
То же самое - для треугольника АМС
∠1/2 А+ ∠1/2 С+ ∠АМС=180°
Но по условию ∠АМС=3∠В, поэтому
∠1/2 А+ ∠1/2 С+ 3∠В=180°
Из треугольника АВС
∠А +∠С=180 -∠В
Найдем сумму половин углов А и С
(∠А +∠С):2=(180°-∠В):2
Подставим значение суммы половин углов А и С в уравнение для треугольника АМС
(180° -∠В):2 + 3∠В=180°
Умножим обе стороны уравнения на 2, чтобы избавиться от дроби:
180° -∠В +6∠В=360°
5∠В=180°
∠В=180°:5=36°
15.
Т.к. CM-биссектриса прямого угла => ∡ACM=∡MCB=45°
Находи угол в треугольнике ACM:
180-38-45=97°
Находим меньший угол образованный биссектрисой и гипотенузой:
180-97=83°
16.
Сумма углов в треугольнике равна 180° =>
2х+5х+11х=180
18х=180/÷18
х=10
Находим больший угол треугольника:
11·10=110°
17.
Подобно 16 задаче:
3х+5х+7х=180
15х=180/÷15
х=12
Находим меньший угол:
3·12=36°
18.
∡А=2В
∡С=А-10°=2B-10°
Суммы углов равна 180°:
∡A+∡B+∡C=180°
2B+B+2B-10°=180°
5B=190°
∡B=38°
19.
Подобно 18:
∡P=3M=3(K-40°)
∡K=M+40° => ∡M=K-40°
3(K-40°)+K+K-40=180°
3K-120°+K+K-40°=180°
5K=340°
∡K=68°
20.
Сначала найдем углы по подобию 16 задачи:
х+2х+3х=180°
6х=180
х=30°
∡M=30° против него стоит сторона PT=18, по свойству углов в прямоугольном треугольнике, катет лежащий против угла в 30°, равен половине гипотенузы, т.к. MT-гипотенуза, то она равна 18·2=36
32.
Свойства диагоналей ромба:
1. Они перпендикулярны
2. Делят углы ромба пополам.
Диагонали ромба образовывают 4 прямоугольных треугольника:
Рассмотрим ΔABO:
Зная больший угол в ромбе найдем больший острый угол в треугольнике:
110:2=55°
Сумма углов треугольника 180
180-90-55=35
Это и есть меньший угол образованный диагональю и стороной ромба.
33.
ΔADC-равнобедренный:
Сумма углов в треугольнике 180°
∡ADC-больший в ромбе
∡ADC=180-43-43=94°
34.
Все стороны ромба равны=> ΔABD-равносторонний.
Все его углы равны 60°.
Значит больший угол ромба равен 60+60=120°
36.
ABCO-ромб сумма его углов равна 360°
Т.к. AC и СВ- касательные к окружности и ОА, ОВ радиусы, а они к ним перпендикулярны, то ∡OAC=∡CBO=90°
Зная 3 угла можно найти 4:
∡AOB=360-180-76=104°
37.
На подобии 36 задачи находим центральный угол, после чего вписанный:
Центральный угол(MON) равен 132°
Вписанный угол(MCN) равен половине центрального угла(MON).
132:2=66°
38.
Точно так же как 37:
Центральный угол равен 144°
Вписанный равен 72°.
39.
По свойству вписанного четырехугольника в окружность, сумма противоположных углов равна 180°
Значит величина угла лежащего напротив большего равна:
180-112=68°
40.
На подобии 39 и 16:
2х+3х=180°
5х=180°
х=36
Чтобы найти меньший умножаем на 2:
36·2=72°
41.
Больший угол равен 144.
Т.к. эти углы вписанные они равны половине дуги на которую они опирается.
Значит чтобы найти дугу умножаем больший угол на 2:
144·2=288°
42.
∡ABC-вписанный, он опирается на ту же дугу что и центральный угол(AOC), значит он равен половине центрального.
59·2=118°
Это и есть ∡AOC.