Предмет: Алгебра,
автор: dasew12
исследуйте функцию f(x)=√3-2x-x^2 постройте ее график
Ответы
Автор ответа:
8
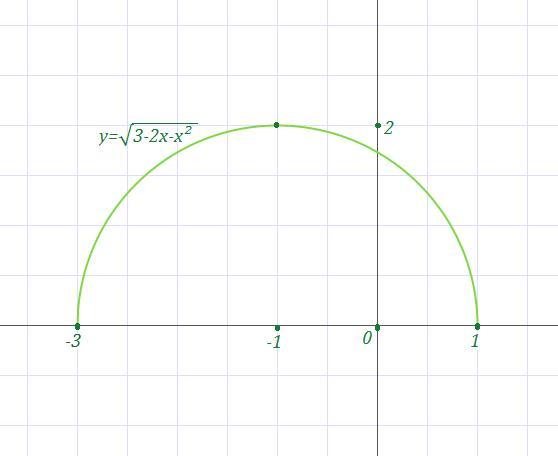
Дана функция у = √(3 - 2x - x²).
Возведём обе части в квадрат.
у² = 3 - 2x - x².
Перенесём правую часть влево.
x² + 2x + у² - 3 = 0. Сделаем группировку:
(x² + 2x + 1) - 1 + у² - 3 = 0. И получаем уравнение окружности.
(х + 1)² + у² = 2².
Но поскольку в исходном уравнение дан только арифметический корень, то график заданной функции - полуокружность радиуса 2 с центром в точке (-1; 0) в положительной полуплоскости.
Автор ответа:
11
это полуокружность с центром в точке ( -1,0) , радиуса R=2, расположенная в верхней полуплоскости .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: omeragayev521
Предмет: Математика,
автор: AlisaFoxsa
Предмет: Немецкий язык,
автор: minura8000
Предмет: Литература,
автор: SashaGorlov
Предмет: Математика,
автор: Таля111